См. также: Прикладная математическая статистика (материалы к семинарам)

 

Заводская лаборатория, 1998. Т. 64. - №1. - С.56-64.

 

УДК 519.24

Асимптотически оптимальное группирование наблюдений в критериях согласия

 

Б.Ю. Лемешко

 

            Казалось бы, что вследствие того, что при группировании наблю­дений происходит потеря информации, такой критерий как c2 Пир­сона должен всегда уступать по мощности, например, непараметрическим кри­териям согласия. На самом деле, при соответствующем способе группи­рования, связанном с видом распределения, согласие с которым проверя­ется, критерии типа c2 могут лучше, чем те же непараметрические, улав­ливать в выборочных данных небольшие отклонения от предположений (отклонения вида закона, наличие грубых ошибок или засорение выборки наблюдениями, принадлежащими другому закону). Если в задаче оце­нивания параметров закона распределения группирование наблюдений при­водит к робастным оценкам [1,2] и наиболее устойчивыми оказываются оцен­ки при равновероятном группировании, то напротив наибольшая чув­ствительность критериев согласия к близким альтернативам проявляется при асимптотически оптимальном группировании, минимизирующем потери в информации Фишера о законе распределения. Целью данной статьи является стремление показать, как отражается такое группирование на ре­зультатах проверки гипотез, и настоятельно рекомендовать применение по­лу­ченных таблиц или соответствующих подходов в практике статис­ти­ческого анализа.

            Целый ряд критериев согласия или критериев проверки гипотез о принадлежности функции распределения независимых одинаково распре­деленных случайных величин  семейству непрерывных функций , зависящих от пара­мет­ра , в общем случае векторного, пред­усматривает группирование наблю­дений. Область опре­деления случайной величины разби­вается на  непересекающихся интервалов граничными точками

,

где  - нижняя грань области определения случайной ве­ли­чины,  - верхняя грань. В результате получают количества наблюдений , попав­ших в -й интервал значений, и соответствующие вероятности попадания в интервал 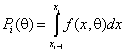, где  - функция плотности рас­пре­де­ления, , где  - объем выборки, . Измерение откло­нений  от  лежит в основе статистик, используемых в критериях согласия.

            К критериям такого рода, в частности, относятся критерий c2 Пир­сона, критерий отношения правдоподобия [3] и критерии типа c2 [4-6].

            Очевидно, что группирование наблюдений приводит к потере инфор­мации, и эти потери зависят от выбора варианта группировки данных. На практике обычно строят интервалы рав­ной длины или, в лучшем случае, ин­тервалы равной вероятности. Потери информации о законе распре­де­ления в этих ситуациях различны и раз­лична способность критериев распо­знавать близкие гипотезы.

            Мерой внутренней близости рас­пределений случайных величин слу­жит фишеровская информация, и этот внутренний характер связан с мощ­ностью различения между близкими значениями параметра. Так как в лю­бой ста­тистике не больше информации, чем в исходной выборке, то мощность различения с по­мощью статистики не больше, чем с помощью всей выборки. Следовательно, если нужно выбирать между несколькими статистиками, следует пред­почесть ту, для которой потери фишеровской информации мини­мальны [7, с.299-300].

            Статистика критерия согласия c2 Пирсона вычисляется в соответ­ствии с соотношением

                        (1)

и в пределе подчиняется c2 -распределению с -й степенью свободы, если верна нулевая гипотеза. Эта же статистика подчиняется нецен­тральному c2 -рас­пределению с тем же числом степеней свободы и параметром нецен­тральности

,

если верна конкурирующая гипотеза, и выборка соответствует распре­делению того же типа, но с параметром .

            Несложно показать, разлагая  в ряд Тейлора при малых  и пренебрегая членами высшего порядка, что

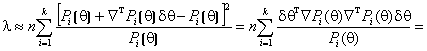
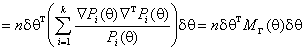,           (2)

где  - информационная матрица Фишера по груп­пированным данным. Мощность критерия c2  Пирсона представляет собой неу­бы­вающую функцию от . Матрица потерь информации, вы­званных группированием, , где  - информа­ционная матрица Фишера по не­груп­пированным наблюдениям, является неотри­цательно определённой, и, следовательно, . А так как  , то очевидно, что с ростом потерь информации падает и мощ­ность критерия при близких альтер­нативных гипотезах.

            В критерии отношения правдоподобия используется статистика вида [3, с.559-562]

,

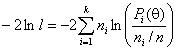которая при верной нулевой гипотезе асимптотически распре­делена как c2  с -й степенью свободы. Если верна конкурирующая гипотеза и выборка принадлежит рас­пределению того же типа, но с параметром , мерой близости рас­сматриваемых распределений явля­ется величина

.

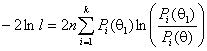С ростом её увеличивается мощность критерия. Действуя как и в пред­ы­дущем случае и пренебрегая членами высшего поряд­ка, будем иметь

.

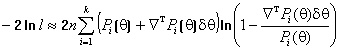Далее, раскладывая  по формуле Тейлора и вновь пренебрегая члена­ми выше второго порядка, получаем

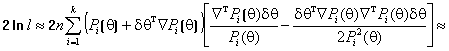
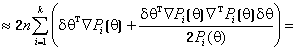
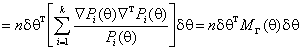.            (3)

Это соотношение аналогично выражению (2).

            Если оценки параметров находились в результате минимизации ста­тистики , то  асимптотически распределена как c2  с числом степеней свободы , где  - количество оцененных по данной выборке па­ра­метров. Если же параметры оцениваются по негруппи­ро­ванным наблю­дениям, например, методом максимального правдоподобия, то эта статистика распределена в пределе как сумма независимых сла­га­емых , где  - стандартные нормальные слу­чай­ные величины, независимые между собой и с , а  - не­которые числа между 0 и 1 [8,9,4]. Распре­де­ление этой суммы лежит между распределениями  и . Поэтому, принимая нулевую гипотезу, на практике ста­раются удостове­риться, что статистика  не превышает критических зна­чений  и , где  - задаваемый уровень значимости. И если <<, то, принимая или от­клоняя гипотезу о согласии, мы можем с одинаковым риском совершить ошибку.

            В работах [4-6] рекомендуется видоизменение стандартной ста­тис­тики , при котором предельное распределение есть обычное рас­пре­деление  c2  с -й степенью свободы и в том случае, когда в ка­чес­тве оценок используются оценки максимального правдоподобия пара­мет­ров по негруппированным данным. При этом вектор  предпо­ла­га­ется заданным и граничные точки интервалов определяются соот­­ноше­ниями , . Предложенная статис­тика имеет вид [5]

,

где  вычисляется в соответствии с (1), ,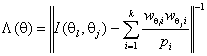

элементы и размерность которой определяются оцениваемыми компонен­тами вектора параметров ,  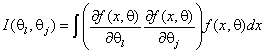- эле­менты информационной матри­цы Фишера по негруппированным данным ,  - элементы вектора , . В данном случае спра­вед­ливо соотношение

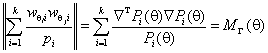
и, следовательно,

.                        (4)

            Таким образом, как и в соотношениях (2)-(3) в данном случае пара­метр нецентральности предельного нецентрального  распределения (см. [5]) зависит от величины потерь информации при группировании. Следовательно, чем меньше потери информации, связанные с груп­пи­ро­ванием наблю­дений, тем выше мощность соответствующих критериев со­гласия при близ­ких конкурирующих гипотезах. Потери от группирования можно умень­шить, под­бирая гранич­ные точки так, чтобы  стреми­лась к инфор­мационной матрице по негруппи­ро­ван­ным данным , т.е., как и при оценивании параметров, решая зада­чу асимп­тотически опти­­мального группирования. В случае скалярного пара­метра эта задача сво­дится к максимизации информационного количества Фишера о пара­метре по группированной выборке

.

А в случае вектора параметров в качестве критериев оптимальности могут быть выбраны различные функционалы от инфор­мационной матрицы Фи­шера. Например, как это делалось в настоящем случае, можно максими­зировать определитель инфор­маци­онной матрицы, т.е. решать задачу

.

            К сожалению, на практике наиболее часто, применяя критерий c2  Пирсона, используют интервалы равной длины или, в лучшем случае, ин­тервалы равной вероятности. Естественно, что в такой ситуации мощность критерия обычно далека от максимально возможной.

            Для иллюстрации на рис. 1 приведены построенные функции мощ­ности критерия c2  при проверке согласия с экспоненциальным распре­делением для числа интервалов , объеме выборки , при уровне значимости  в случае асимптотически оптимального груп­пирования и разбиения на интервалы равной вероятности. При построении кривых были исполь­зованы таблицы мощности критерия c2  из [10]. Гра­фики наглядно иллю­стрируют предпочтительность асимптотически опти­маль­ного груп­пи­рования.

            В общем случае информационная матрица Фишера зависит не только от граничных точек , но и от параметров иссле­ду­емого распределения. Однако для достаточно широкого ряда распреде­ле­ний при решении задач асимптотически оптимального группирования уда­лось получить граничные точки интервалов в виде, инвариантном относительно параметров распределений, и на их основе сформировать таблицы асимптотически оптимального группирования. В связи с проблемой оценивания пара­метров по группированным выборкам задача асимптотически оптимального группирования данных рас­сматривалась в [11,12], неоднократно она воз­никала при использовании для оценивания параметров выборочных кван­тилей. Наиболее пол­ная совокупность таблиц асимптотически оптимального группирования для распре­делений экспо­ненциального, полунормаль­ного, Рэлея, Максвелла, модуля много­мер­ного нормального вектора, Парето, Эрланга, Лапласа, нормального, логарифми­чески-нормальных (ln и lg), Коши, Вейбулла, распределений минималь­ного и максимального значения, двойного пока­зательного, гамма-распределения представлена в [13]. В общей сложности получено 54 таблицы оптимальных граничных точек и соответствующих вероятностей. Эти таблицы могут использоваться как при проверке гипотез, так и при оценивании. Полученные таблицы используются в про­граммной системе [14] при проверке согласия по критериям c2  Пирсона и отношения правдоподобия и при вычислении робастных оценок.

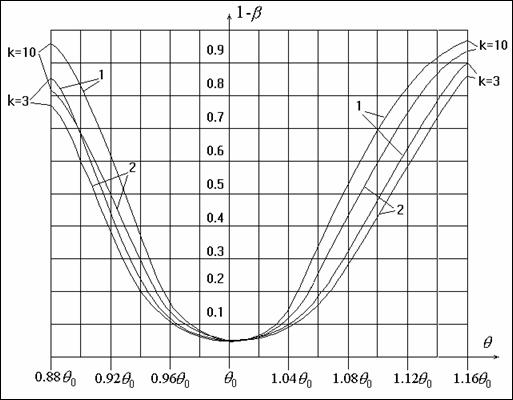
Рис. 1. Функция мощности критерия c2  для уровня значимости

, объема выборки , числа интервалов :

     1 - для оптимального группирования; 2 - для равновероятного группирования.

 

            В табл. 1 представлены асимп­тотически опти­маль­ные граничные точки интервалов в виде  при проверке гипотез о согласии с нормальным распределением с плотностью

.

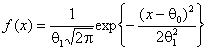Они были получены максимизацией определителя информационной мат­рицы Фишера по группированным наблюдениям. При проверке гипотезы о согласии с нормальным распределением с параметрами  и  кон­крет­ные значения  определятся соотношением . Вероятности попадания наблюдений в интервалы, соответ­ству­ю­щие оптимальному груп­пированию, представлены в табл. 2. Содержащиеся в табл. 1 граничные точки интервалов рекомендуется использовать в случаях, когда по выборке или не оценивались параметры нормального распределения, или оцени­ва­лись сразу оба. Если же по наблюдаемой выборке оценивался только один из параметров, то должно быть использовано группирование, максимизи­ру­ющее количество информации по группиро­ван­ным данным для оцени­ваемого параметра. Соответствующие таб­лицы приведены в [13].

            Эти же таблицы могут использоваться для логарифмически нор­мального распределения с плотностью

.

В этом случае граничные точки интервалов будут определяться соотно­шением . Для логарифмически нормального закона с плотностью

граничные точки вычисляются в соответствии с выражением . В последних колонках приведенных таблиц содержатся значения отно­си­тельной асимптотической информации , позволя­ющей судить о качестве группирования.

            В табл. 3 представлены асимптотически оптимальные граничные точ­ки интервалов в виде  для проверки согласия с распре­делением Вейбулла с плотностью

.

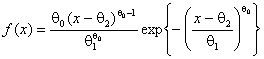Соответствующие значения вероятностей представлены в табл. 4. Эти таблицы рекомендуется использовать в случаях, когда по выборке не оценивались параметры распределения, или одновременно оцени­ва­лись параметры  и . Конкретные значения граничных точек определяются соотношением . Если по имеющейся выборке оценивался только один из указанных параметров, то рекомендуется использовать таб­лицы, приве­денные в [13], в которых при группировании максимизи­ро­валось количество информации по группиро­ван­ным данным для соответ­ству­ющего параметра.

            Аналогичным образом табл. 3-4 могут использоваться в критериях проверки согласия с распределением наименьшего экстремаль­ного значения с плотностью

.

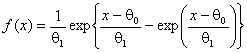В этом случае конкретные значения граничных точек будут определяться выражением .

            Для многих законов распределений граничные точки интервалов не мо­гут быть выражены в виде, инвариантном относительно параметров рас­пре­­делений, т.е. они остаются функциями этих параметров. Это касается, например, таких законов, как гамма- и бета-распределения [15,16], экспо­ненциального семейства распределений. В этом случае формирование таб­лиц асимпто­тически оптимального группирования теряет смысл. Однако воз­­можно решение задачи асимптотически оптимального группирова­ния при конкретных значениях параметров в процессе проверки гипотез о со­гласии, как это реализуется в таких ситуациях в программной системе [14].

            Продемонстрируем, как практически отражается применение асимп­то­тически оп­ти­­мального группирования на результатах статистического анализа при различных отклонениях выборки от предположений.

Пример 1. На рис. 2 приведены результаты моделирования выборки объемом  в соответствии с логистическим распределением с функ­цией плотности

,

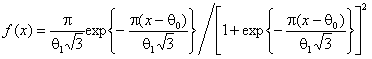и параметрами . При проверке согласия использовано асимп­тотически оптимальное группирование при числе интервалов . На этом и последующих рисунках для параметров распределений использо­ваны обозначения , , , На рисунках отражаются результаты про­верки гипотез о согласии: вычис­ленные значения  соот­ветствующих ста­тистик  и вероятности пре­вы­­шения полученного значения статистики при истинности нулевой гипоте­зы . Гипотеза о согла­сии не отверга­ется, если . Проверка согласия осущес­твля­ется по критериям отношения правдоподобия,  Пирсона, применение ко­торых предусматривает группирование наблюдений, а также по непара­метрическим критериям Колмогорова, Смирнова,  и  Мизеса [8]. Статистику критерия  называют статистикой Смирнова-Мизеса, ста­тис­тику  - Андерсона-Дарлинга.

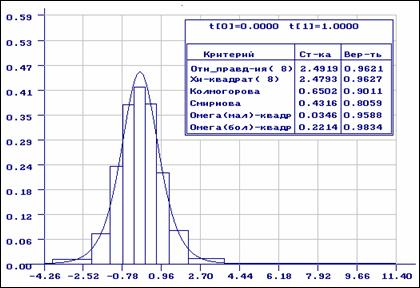
Рис.2. Результаты моделирования логистического

распределения

 

            Посмотрим, что получится, если мы будем проверять согласие полу­чен­ной выборки с нормальным распределением с параметрами , . На рис. 3 представлены результаты проверки согласия при исполь­зовании в критериях отношения правдоподобия и c2  Пирсона равнове­роятного груп­пирования. Как видим, по всем критериям, в том числе непарамет­ри­ческим, при уровне значимости  нет оснований для отклонения гипотезы о согласии.

 

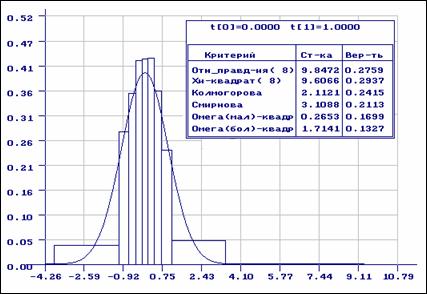
Рис.3. Результаты проверки согласия выборки, распределенной по логис­­ти­­чес­кому закону, с нормальным распределением (равновероятное группирование)

 

            Результаты анализа, приведенные на рис. 4 отличаются тем, что в критериях отношения правдоподобия и c2  Пирсона использовалось асимп­тотически оптимальное группирование (табл. 1-2, ). В этом случае гипотеза о согласии при  должна быть отклонена. В данном примере логистическое и нормальное распределения имеют отличие в середине области определения.

 

 

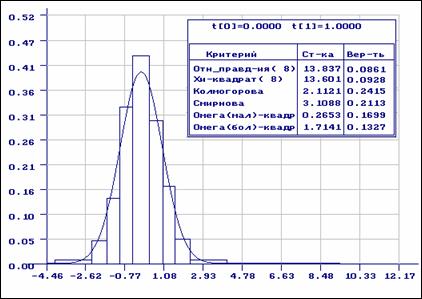
Рис.4. Результаты проверки согласия выборки, распределенной по логистическому закону, с нормальным распределением

(асимптотически оптимальное группирование)

 

Пример 2. На рис. 5 приведены результаты моделирования выборки объемом  в соответствии с распределением Лапласа с плотностью

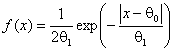
и параметрами . Было высказано предположение, что наблю­даемая выборка принадлежит нормальному закону с параметрами , . Результаты проверки согласия с нормальным распределением представлены на рис. 6-7. Результатам анализа на рис. 6 соответствовало равновероятное группирование в критериях согласия при числе интер­валов , а на рис. 7 - асимптотически оптимальное группирование (табл. 1-2, ).  Как видим, в первом случае гипотеза о согласии будет при­нята, если уровень значимости , во втором - по критериям отношения правдо­подобия и c2  Пирсона гипотеза о согласии должна быть отклонена. В отличие от предыдущего примера рассматриваемые здесь распре­деления отличаются на “хвостах”.

 

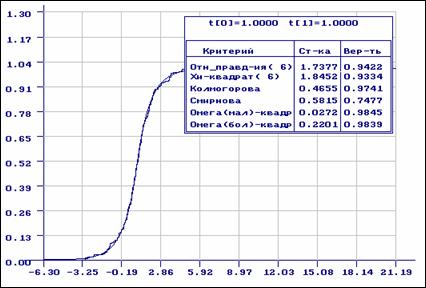
Рис.5. Результаты моделирования распределения Лапласа:

эмпирическая функция и функция распределения Лапласа

 

 

 

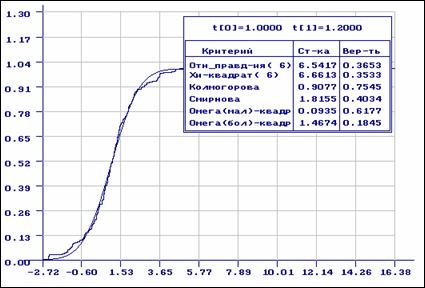
Рис.6. Результаты проверки согласия выборки, распределенной

по закону Лапласа, с нормальным распределением: эмпирическая

функция и функция распределения нормального закона

(равновероятное группирование)

 

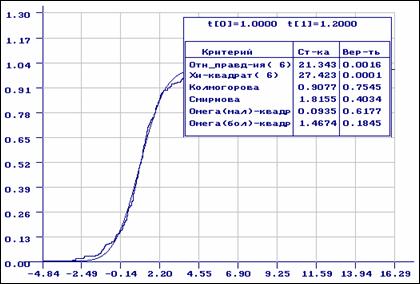
Рис.7. Результаты проверки согласия выборки, распределенной

по закону Лапласа, с нормальным распределением: эмпирическая

функция и функция распределения нормального закона

(асимптотически оптимальное группирование)

 

Пример 3. Выборка объёмом 200 наблюдений, смодели­рованная в соответствии с распределе­нием Вейбулла с параметрами , , , была “засорена” 10 наблюдениями нормального закона с пара­метрами . При анализе в данном примере осуществлялось группирование для числа интервалов . На рис. 8 отражены резуль­таты проверки согласия “смеси” с исходным рас­пределением Вейбулла при использовании равновероятного группирования, а на рис. 9 - асимп­то­ти­чески оптимального (табл. 3-4, ). На рис. 10 приведены функция распределения Вейбулла и эмпирическая функция “смеси”. Как видим, и в данном случае при асимптотически оптимальном группировании критерии отношения правдоподобия и  Пирсона улавливают наличие отклонений от пред­положений.

            Три приведенных примера демонстрируют чувствительность крите­ри­ев согласия при асимптотически оптимальном группировании к раз­лич­ным отклонениям выборки от предположений. Но это совсем не означает, что при оптимальном группировании вероятности вида  для рассмат­риваемых критериев всегда меньше, чем при равновероятном. Если выбор­ка действительно принадлежит данному закону (хорошо согласуется), то эти вероятности при оптимальном группировании часто оказываются боль­ше, чем при равновероятном.

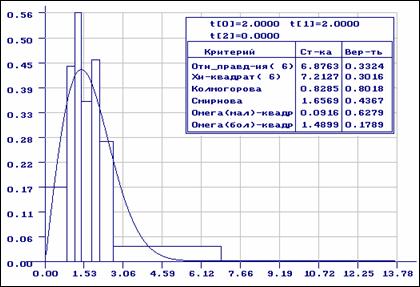
Рис.8. Результаты проверки смеси с распределением Вейбулла с параметрами  (равновероятное группирование)

 

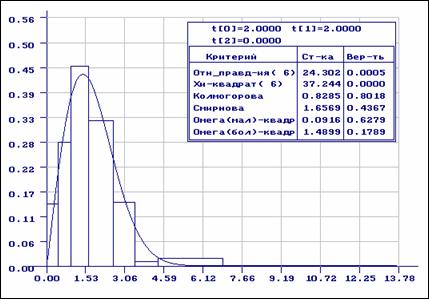
Рис.9. Результаты проверки смеси с распределением

Вейбулла с параметрами

(асимптотически оптимальное группирование)

 

Пример 4. На рис. 11 и 12 приведены результаты проверки согласия выборки объемом 1000 наблюдений, смоделированной в соответствии с распределением Вейбулла с параметрами  , , : на рис. 11 при оптимальном, а на рис. 12 при равновероятном группировании. В данном случае при оптимальном группировании согласие по критериям отношения правдоподобия и c2  Пирсона лучше, чем при равновероятном. При оптимальном группировании граничные точки при числе интервалов c2  вычислялись в соответствии с соотношениями , где  были взяты из табл. 3 при , а значения  выбирались из соответствующей строки табл. 4.

 

 

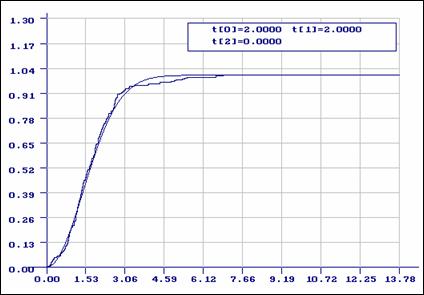
Рис.10. Эмпирическая функция распределения “смеси” и теоретическая функция распределения Вейбулла с параметрами

 

 

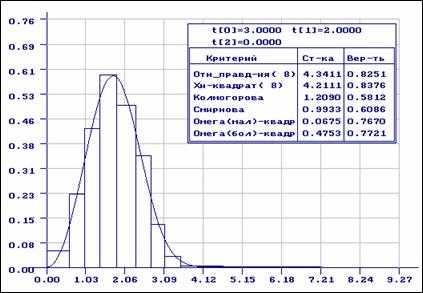
Рис.11. Результаты проверки согласия выборки, смоделированной с распределением Вейбулла с параметрами  при асимптотически оптимальном группировании

 

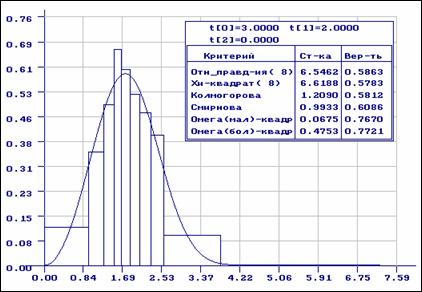
Рис.12. Результаты проверки согласия выборки, смоделированной с распределением Вейбулла с параметрами  при равновероятном группировании

Таблица 1.

Оптимальные граничные точки интервалов при проверке гипотез о согласии по критериям  Пирсона и отношения правдоподобия (или при одновременном оценивании двух параметров распределения) в виде  для нормального распределения, в виде  и  для лога­риф­мически нормальных распределений и соответствующие значения относительной асимптотической информации

3

-1.1106

1.1106

 

 

 

 

 

4

-1.3834

0.0

1.3834

 

 

 

 

5

-1.6961

-0.6894

0.6894

1.6961

 

 

 

6

-1.8817

-0.9970

0.0

0.9970

1.8817

 

 

7

-2.0600

-1.2647

-0.4918

0.4918

1.2647

2.0600

 

8

-2.1954

-1.4552

-0.7863

0.0

0.7863

1.4552

2.1954

9

-2.3188

-1.6218

-1.0223

-0.3828

0.3828

1.0223

1.6218

10

-2.4225

-1.7578

-1.2046

-0.6497

0.0

0.6497

1.2046

11

-2.5167

-1.8784

-1.3602

-0.8621

-0.3143

0.3143

0.8621

12

-2.5993

-1.9028

-1.4914

-1.0331

-0.5334

0.0

0.5334

13

-2.6746

-2.0762

-1.6068

-1.1784

-0.7465

-0.2669

0.2669

14

-2.7436

-2.1609

-1.7092

-1.3042

-0.9065

-0.4818

0.0

15

-2.8069

-2.2378

-1.8011

-1.4150

-1.0435

-0.6590

-0.2325

 

 

 

 

 

 

 

 

 

0.4065

 

 

 

 

 

 

 

0.5527

 

 

 

 

 

 

 

0.6826

 

 

 

 

 

 

 

0.7557

 

 

 

 

 

 

 

0.8103

 

 

 

 

 

 

 

0.8474

2.3188

 

 

 

 

 

 

0.8753

1.7578

2.4225

 

 

 

 

 

0.8960

1.3602

1.8784

2.5167

 

 

 

 

0.9121

1.0331

1.4914

1.9028

2.5993

 

 

 

0.9247

0.7465

1.1784

1.6068

2.0762

2.6746

 

 

0.9348

0.4818

0.9065

1.3042

1.7092

2.1609

2.7436

 

0.9430

0.2325

0.6590

1.0435

1.4150

1.8011

2.2378

2.8069

0.9498

 

Таблица 2.

Оптимальные частоты при проверке гипотез о согласии по критериям  Пирсона и отношения правдоподобия (или при одновременном оценивании двух параметров) для нор­мального и лога­риф­мически нормальных распределений и соответствующие значения относительной асимптотической информации

3

0.1334

0.7332

0.1334

 

 

 

 

 

4

0.0833

0.4167

0.4167

0.0833

 

 

 

 

5

0.0449

0.2004

0.5094

0.2004

0.0449

 

 

 

6

0.0299

0.1295

0.3406

0.3406

0.1295

0.0299

 

 

7

0.0197

0.0833

0.2084

0.3772

0.2084

0.0833

0.0197

 

8

0.0141

0.0587

0.1431

0.2841

0.2841

0.1431

0.0587

0.0141

9

0.0102

0.0422

0.1009

0.1976

0.2982

0.1976

0.1009

0.0422

10

0.0077

0.0317

0.0748

0.1438

0.2420

0.2420

0.1438

0.0748

11

0.0059

0.0243

0.0567

0.1074

0.1823

0.2468

0.1823

0.1074

12

0.0047

0.0190

0.0442

0.0829

0.1392

0.2100

0.2100

0.1392

13

0.0037

0.0152

0.0352

0.0652

0.1085

0.1670

0.2104

0.1670

14

0.0030

0.0124

0.0283

0.0524

0.0862

0.1327

0.1850

0.1850

15

0.0025

0.0101

0.0232

0.0427

0.0698

0.1066

0.1532

0.1838

 

 

 

 

 

 

 

 

 

0.4065

 

 

 

 

 

 

 

0.5527

 

 

 

 

 

 

 

0.6826

 

 

 

 

 

 

 

0.7557

 

 

 

 

 

 

 

0.8103

 

 

 

 

 

 

 

0.8474

0.0102

 

 

 

 

 

 

0.8753

0.0317

0.0077

 

 

 

 

 

0.8960

0.0567

0.0243

0.0059

 

 

 

 

0.9121

0.0829

0.0442

0.0190

0.0047

 

 

 

0.9247

0.1085

0.0652

0.0352

0.0152

0.0037

 

 

0.9348

0.1327

0.0862

0.0524

0.0283

0.0124

0.0030

 

0.9430

0.1532

0.1066

0.0698

0.0427

0.0232

0.0101

0.0025

0.9498

 

Таблица 3.

Оптимальные граничные точки интервалов при проверке гипотез о согласии по критериям  Пирсона и отношения правдоподобия (или при одновременном оценивании двух параметров распределения) в виде  для распределения Вейбулла, в виде для распределения наименьшего экстремального значения и соответствующие значения относительной асимптотической информации

3

0.2731

2.6067

 

 

 

 

 

 

4

0.2109

1.3979

3.4137

 

 

 

 

 

5

0.1044

0.5123

1.9590

3.8606

 

 

 

 

6

0.0772

0.3649

1.2269

2.5726

4.4096

 

 

 

7

0.0501

0.2318

0.6758

1.7192

2.9922

4.7959

 

 

8

0.0377

0.1740

0.4837

1.1904

2.2041

3.4285

5.2049

 

9

0.0275

0.1269

0.3431

0.7829

1.6027

2.5713

3.7667

5.5273

10

0.0213

0.0988

0.2638

0.5770

1.1805

1.9932

2.9269

4.1024

11

0.0165

0.0771

0.2046

0.4359

0.8560

1.5344

2.3192

3.2319

12

0.0123

0.0618

0.1638

0.3434

0.6517

1.1789

1.8570

2.6163

13

0.0106

0.0500

0.1326

0.2754

0.5106

0.9030

1.4807

2.1401

14

0.0087

0.0412

0.1094

0.2261

0.3126

0.7116

1.1798

1.7608

15

0.0072

0.0344

0.0913

0.1881

0.3394

0.5734

0.9387

1.4426

 

 

 

 

 

 

 

0.4079

 

 

 

 

 

 

0.5572

 

 

 

 

 

 

0.6836

 

 

 

 

 

 

0.7571

 

 

 

 

 

 

0.8109

 

 

 

 

 

 

0.8480

 

 

 

 

 

 

0.8756

5.8478

 

 

 

 

 

0.8963

4.3930

6.1270

 

 

 

 

0.9123

3.5103

4.6589

6.3853

 

 

 

0.9248

2.8810

3.7623

4.9016

6.6208

 

 

0.9349

2.4019

3.1286

3.9997

5.1314

6.8444

 

0.9431

2.0116

2.6381

3.3538

4.2169

5.3425

7.0506

0.9498

 

 

Таблица 4.

Оптимальные частоты при проверке гипотез о согласии по критериям  Пирсона и отношения правдоподобия (или при одновременном оценивании двух параметров) для распределений Вейбулла и наименьшего экстре­мального значения и соответствующие значения относительной асимптотической информации

3

0.2390

0.6872

0.0738

 

 

 

 

 

4

0.1901

0.5628

0.2142

0.0329

 

 

 

 

5

0.0991

0.3018

0.4581

0.1199

0.0211

 

 

 

6

0.0743

0.2314

0.4011

0.2169

0.0641

0.0122

 

 

7

0.0489

0.1581

0.2843

0.3295

0.1290

0.0419

0.0083

 

8

0.0370

0.1227

0.2238

0.3124   

0.1938

0.0779

0.0269

0.0055

9

0.0271

0.0921

0.1712

0.2525

0.2557

0.1250

0.0533

0.0191

10

0.0211

0.0729

0.1379

0.2065

0.2545

0.1708

0.0827

0.0371

11

0.0164

0.0578

0.1108

0.1683

0.2218

0.2101

0.1164

0.0589

12

0.0131

0.0468

0.0912

0.1395

0.1882

0.2136

0.1515

0.0830

13

0.0105

0.0383

0.0754

0.1165

0.1592

0.1947

0.1779

0.1099

14

0.0087

0.0317

0.0632

0.0988  

0.1357

0.1710

0.1836

0.1354

15

0.0072

0.0266

0.0535

0.0842

0.1163

0.1486

0.1725

0.1548

 

 

 

 

 

 

 

 

 

0.4079

 

 

 

 

 

 

 

0.5572

 

 

 

 

 

 

 

0.6836

 

 

 

 

 

 

 

0.7572

 

 

 

 

 

 

 

0.8109

 

 

 

 

 

 

 

0.8480

0.0040

 

 

 

 

 

 

0.8756

0.0136

0.0029

 

 

 

 

 

0.8963

0.0271

0.0102

0.0022

 

 

 

 

0.9123

0.0432

0.0204

0.0078

0.0017

 

 

 

0.9248

0.0615

0.0329

0.0158

0.0061

0.0013

 

 

0.9349

0.0814

0.0467

0.0255

0.0124

0.0048

0.0011

 

0.9431

0.1025

0.0623

0.0365

0.0203

0.0099

0.0039

0.0009

0.9498

 

Выводы

1.      Применение асимптотически оптимального группирования данных в критериях согласия отношения правдоподобия, c2  Пир­сона и типа c2  обеспечи­вает максимальную мощность этих критериев при близких конкурирующих гипотезах. Следовательно, снижается риск принятия нулевой гипотезы, когда на самом деле выборка принадлежит неко­торому другому закону. Для практического применения асимптотически оптимального группирования в критериях согласия могут использоваться таблицы, приведенные в [13,17].

2.      Таблицы асимптотически оптимального группирования могут исполь­зоваться не только в задачах проверки гипотез о согласии, но и при получении различных оценок параметров, использующих выборочные квантили.

3. Выбор числа интервалов. По этому поводу в свое время проводилось немало исследований, существует достаточно много противоречивых ре­комендаций, часть из которых приведена в [18]. При асимптотически оптимальном группировании относительно скалярного параметра при 10-11 интервалах в груп­пированной выборке сохраняется около 98% информации, при опти­мальном группировании относительно вектора параметров (два пара­метра) для 15 интервалов - около 95%. Даль­нейшее увеличение количества интервалов существенного значения не имеет. Выбор конкретного числа интервалов должен осуществляться из следующих соображений. При оптимальном группировании вероятности попадания в интервалы в общем случае не равны. Обычно минимальны вероятности попадания в крайние интервалы. Поэтому  желательно выбирать из условия  для любого интервала при опти­мальном группировании. По крайней мере минимальная ожидаемая частота должна быть больше 1.

4. Множество непрерывных законов распределений, используемых в за­дачах статистического анализа, немногим превышает 100, а для описания наблюдаемых случайных величин в прикладных исследованиях исполь­зуется порядка 30 законов и семейств распределений. Естественно, что это не покрывает того многообразия случайных величин, которое встре­чается на практике. Правильное применение критериев согласия часто приводит и должно приводить к отклонению гипотез о при­надлежности выборки удобному и привычному закону распределения, например нормальному. Это подталкивает к выводу о тупиковой ситуации в параметрической статистике, призывам к отказу от пара­метрических методов. Можно взглянуть на эту проблему по-другому. Законы реальных случайных величин, которые являются следствием большого числа причин, сложнее тех моделей, которые используются для их описания. Следовательно, и модели должны быть более сложными. В частности, положительных результатов в приложениях можно добиться, используя в качестве моделей смеси различных законов распределений, в том числе усеченных [19].

 

Литература

 

1.         Лемешко Б.Ю. Робастные методы оценивания и отбраковка ано­маль­ных изме­рений // Заводская лаборатория, 1997. Т.63. № 5. - С. 43-49.

2.         Лемешко Б.Ю. Группирование наблюдений как способ полу­чения ро­бастных оценок // Надежность и контроль качества, 1997. № 5. - С. 26-35.

3.         Кендалл М., Стьюарт А. Статистические выводы и связи. - М.: Наука, 1973. - 900 с.

4.         Никулин М.С. Критерий хи-квадрат для непрерывных распределений с параметрами сдвига и масштаба / Теория вероятностей и ее приме­нение. 1973. Т. XVIII. № 3. С.583-591.

5.         Никулин М.С. О критерии хи-квадрат для непрерывных распре­де­лений / Теория вероятностей и ее применение. 1973. Т. XVIII. № 3. С.675-676.

6.         Мирвалиев М., Никулин М.С. Критерии согласия типа хи-квадрат / Заводская лаборатория. 1992. Т. 58. № 3. С.52-58.

7.      Рао. С.Р. Линейные статистические методы и их применения. - М.: Наука, 1968. - 548 с.

8.      Chernoff H., Lehmann E.L. The use of maximum likelihood estimates in c2  test for goodness of fit // Ann. Math. Stat., 1954. V. 25. - P. 579-586.

9.      Чибисов Д.М. Некоторые критерии типа хи-квадрат для непрерывных распределений // Теория ве­ро­ятностей и ее применение. 1971. Т. XVI. № 1. - С. 3-20.

10.  Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. - М.: Наука, 1983. - 416 с.

11.  Cox D.R. Note on grouping // J. of the Amer. Statist. Ass. 52 (1957) - p. 543-547.

12.  Куллдорф Г. Введение в теорию оценивания по группированным и частично группированным выборкам. - М.: Наука, 1966. - 176 с.

13.     Денисов В.И., Лемешко Б.Ю., Цой Е.Б. Оптимальное группи­рование, оцен­ка параметров и планирование регрессионных экспери­ментов. В 2-х ч. / Новосиб. гос. техн. ун-т. - Ново­сибирск, 1993. - 347 с.

14.     Лемешко Б.Ю. Статистический анализ одномерных наблюдений слу­чай­­ных величин: Программная система. - Новоси­бирск: Изд-во НГТУ,  1995. - 125 с.

15.     Денисов В.И., Зачепа Г.Г., Лемешко Б.Ю. Об асимптотически опти­мальном группировании при оценивании основного параметра гамма-рас­пределения по группированным данным // Применение ЭВМ в опти­мальном планировании и проектировании. - Новоси­бирск, 1974. - С. 50-53.

16.     Лемешко Б.Ю. К вопросу решения задачи асимптотически опти­маль­ного группирования данных при обработке наблюдений, подчи­няющихся бета-распределению // Машинные методы оптимизации, модели­рова­ния и планирования эксперимента. - Новосибирск, 1988. - С. 134-138.

17.  Объектно-ориентированная программная сис­те­ма статистического ана­лиза: Таблицы коэффициентов для оптимальных L-оце­нок параметров сдвига и масштаба по выбо­рочным квантилям больших выборок и таб­ли­цы асимптотически оптимального группиро­ва­ния наблюдений // От­чет по НИР, НГТУ, 1996. № гос. рег. 01.9.70 000550, инв. № 02.9.70 000190. Научн. рук. Лемешко Б.Ю. - 129 с.

18.  Новицкий П.В., Зограф И.А. Оценка погрешностей результатов изме­рений. - Л.: Энергоатомиздат, 1991. - 303 с.

19.  Лемешко Б.Ю., Постовалов С.Н. Статистический анализ смесей распределений по частично группированным данным. // Сб. научных тру­дов НГТУ. - 1995. - №1. С. 25-31.

 

 

[Содержание]