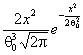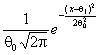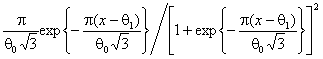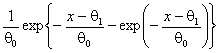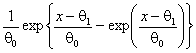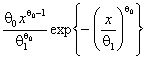См. также: Прикладная математическая статистика (материалы к семинарам)

 

Заводская лаборатория. 1998. Т. 64. - № 3. - С. 61-72.

УДК 519.2

 

О распределениях статистик непараметрических критериев согласия при оценивании по выборкам параметров наблюдаемых законов

 

Б.Ю.Лемешко, С.Н.Постовалов

 

1. Введение и постановка задачи

 

            Наиболее часто в практике статистического анализа с необ­ходи­мос­тью использования критериев согласия приходится сталкиваться после оценивания по этой же выборке параметров предполагаемого закона распределения. К сожалению, в этом случае предельные распределения ста­тистик таких непарамет­ри­ческих критериев, как Колмогорова, Смирнова,  и  Ми­зеса, при справедли­вости нулевой гипотезы вида  , где  - плотность распределения наблюдае­мого зако­на,  - истинное значение параметра,  - оценка параметра, вы­чис­ленная по вы­борке, отличаются от предельных распределений классических статистик (когда по выборке не оце­ниваются пара­метры). При оценивании по выборке параметров рассмат­риваемые критерии теряют свойство “свободы от распределения”, и пре­дельные распределения статис­тик на самом деле зависят как от числа оце­ненных пара­метров, так и от вида исследуемого закона рас­пре­деления . Широкую известность этот фак­т приобрел, начиная с работы [1]. Распространенная ошиб­ка, связанная с пренебрежением существующей проблемы, чаще всего приводит к необо­снованному принятию нулевой гипотезы, что подчеркивается в работах [2,3], из-за сильно завы­шенных значений ве­роятностей “согласия” вида , где  - значение статистики, вы­чис­­­ленное по выборке. И как отмечено в [4], это не всегда учитывается в популярных пакетах статис­тического анализа.

            Если объем выборки достаточно велик, можно, опираясь на ре­зультаты, полученные в [5], оценивать параметры распределения по одной половине выборки, а проверять согласие по другой половине. В такой си­туации применение предельных распределений рассматриваемых кри­териев вполне обосновано. Но в этом случае, как при оценивании, так и при про­верке согласия мы используем только половину имеющейся инфор­мации, что, естественно, сказывается на качестве статистических выводов. К тому же, объемы выборок, зачастую имеющиеся в распоряжении иссле­дователя, не настолько велики, чтобы можно было смириться с потерей части инфор­мации при оценивании параметров.

            Таким образом, с одной стороны некорректность использования клас­сических непараметрических критериев в задачах проверки сложных гипо­тез из-за слишком больших вероятностей ошибок, с другой стороны свой­ства асимп­то­тической оптимальности критериев типа Колмогорова-Смирнова и  (по Ходжесу-Леману) [6] предопределяют необходимость поиска предельных законов распре­деления непараметрических статистик в зави­симости от того, сколько пара­метров оценивалось по выборке и с каким законом прове­ряется согласие.

            Для случая нормального закона предельные распределения статис­тики критерия  Ми­зеса при оце­нивании одного из двух или обоих параметров подробно исследованы в [7], где приведены их таблицы.

            Но очевидно, что теоре­тически найти решение задачи определения пре­дельных распределений непараметрических статистик для множества зако­нов, используемых для описания реальных величин, очень сложно. Именно поэтому большинство существующих таблиц и результатов, свя­занных с предельными распределениями, получены методом статис­тичес­кого моде­ли­рования [8-16]. Таким образом получены, например, таблицы про­цен­тных точек для модифицированных статистик критериев Колмо­горова (типа Кол­мо­горова) при проверке нормальности и оценивании одного или двух параметров нормального распределения и процентные точки при проверке экспоненциальности и оце­нивании его масштабного параметра, пред­став­ленные в [12].

            В работах [17-19] разработан аналитический метод расчета про­цен­тных точек для статистик Колмогорова-Смирнова для регулярных семейств распре­делений и больших выборок, получены фор­мулы для при­бли­жен­ного вычисления вероятностей вида . С по­мощью этих при­бли­женных формул, учитывающих отличие пре­дельных рас­пре­делений не­па­рамет­ри­ческих статистик при оценивании па­ра­метров законов от клас­си­ческих, вычис­ляют вероятности вида  в пакете STADIA [20].

            Нам наи­более реальный выход видится в моделировании предельных зако­нов рас­преде­ления статистик непара­метрических крите­риев и в после­дую­щей иден­ти­фи­кации полученных эмпирических законов. Под иденти­фи­кацией по­ни­мается выбор такого теоретичес­кого закона распределения, который наи­бо­лее хорошо согла­суется с эмпиричес­кой функ­цией распре­де­ления. Резуль­таты такого моде­лирования позво­ля­ют, с одной стороны, количественно оценить возможные ошибки в случае пренебрежения фактом оценивания по выборке параметров наблюдаемого закона, с другой сто­ро­ны, дают воз­можность с достаточной для практики точностью исполь­зо­вать эти результаты при проверке гипотез.

            Реализованный алгоритм числен­ного модели­рования выглядит следу­ющим образом.

1.    Моделируется (имитируется)  выборок заданного объема  в соответ­ствии с задан­ным законом распре­деления .

2.    По каждой выборке оцениваются параметры этого закона распределения (один параметр, или другой, или два одновременно).

3.    Вычисляются значения соответствующих непараметрических ста­тистик.

4.    По накопленной вы­борке значений статистики объема  анализируется полученное эмпирическое распределение статистики и осуществляется его иден­тификация.

            Конечной целью настоящего исследования явилось стремление по воз­можности найти такие за­коны распределения вероятностей, которые с прак­­ти­ческой точки зрения хорошо аппроксимируют предельные распре­деления статистик непарамет­рических критериев в тех случаях, когда по выборке оцениваются пара­метры.

            При постановке задачи исследования планировалось осуществить мо­делирование для различных объемов  и  и, в случае устойчивости полу­ченных результатов, использовать их в программном обеспечении статис­тического анализа [21], а также протабулировать полученные эмпи­ри­ческие законы и критические значения статистик, если не удастся по­добрать подходящего теоретического закона распределения. Подобную процедуру планировалось осуществить для каж­дого закона распределения, вклю­чен­ного в программную систему статис­тического анализа [21].

            В данной статье мы приводим некоторые результаты моделирования и анализа, которые, с нашей точки зрения, могут с успехом применяться при решении практических задач проверки гипотез о согласии с исполь­зо­ванием непараметрических критериев после вычисления оценок параметров распределения по той же выборке.

            Отметим, что результаты моделирования классических непара­метри­ческих статистик (без оценивания параметров) показали хорошее согласие получившихся эмпирических распределений с предельными теоре­ти­ческими законами. Это позво­ляет судить о точности описания пре­дельных законов полученными эмпири­ческими распределениями статистик для ситу­ации с оцениванием параметров, а также служит косвенным под­твер­жде­нием воз­можности использования полученных распределений соот­вет­ству­ющих ста­тистик при решении практических задач статистического анализа.

            Статистика Колмогорова (Колмогорова-Смирнова) определяется вы­ра­жением [22]

,

статистика Смирнова [22]

,

где  

 - объем выборки,  - упорядоченные по возрастанию вы­бо­роч­ные значения,  - функция распределения, согласие с которой про­веряется.

            Распределение величины , если по выборке не оце­нивались па­раметры, в пределе подчиняется закону Колмо­горова с функцией распре­деления  [22].

            Гипотеза о согласии не отвергается, если

,

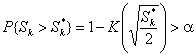где  - задаваемый уровень значимости.

            В аналогичной ситуации статистика Смирнова  подчиняется в пре­деле распределению  с числом степеней свободы, равным 2. Гипотеза о согласии не отвергается, если

.

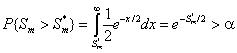            Статистики Мизеса имеют вид [22]

,

которую чаще называют статистикой Крамера-Мизеса-Смирнова, и

,

называемую еще статистикой Андерсона-Дарлинга. Для этих ста­тистик также известны предельные распределения веро­ят­ностей [22]

,

.

            Гипотезы о согласии не отвергаются, если выпол­ня­ются неравенства

  и  .

            В соответствии с изложенным алгоритмом моделировались выборки значений статистик , , , .

            По каждому закону распределения  моделировалась серия из  выборок объемом . Псевдослучайная величина, принад­ле­жащая закону с функцией распределения , имитировалась по методу обратных функций, при котором случайная величина , подчи­няющаяся закону с функци­ей распределения , получается в соот­ветствии с соотношением , где  - функция, обрат­ная к , а  - случайная величина, равномерно распределённая на интервале [0,1]. В качестве датчика равномерно распределенных псевдо­случайных чисел ис­поль­зовался стандартный датчик, реализованный в C++. Оценки пара­метров находились по методу максимального правдо­подобия по не­груп­­пированным данным.

            В данной работе исследовались рас­пределения непараметрических статистик, когда на­блю­даемые случайные величины распре­делены в соот­ветствии с законами, представленными в табл. 1.

 

Таблица 1.

?

п/п

Распределение случайной величины

Функция плотности

1.     

Экспоненци­аль­ное

2.     

Полунор­мальное

3.     

Рэлея

4.     

Максвелла

5.     

Лапласа

6.     

Нормальное

7.     

Логнормаль­ное

8.     

Коши

9.     

Логисти­че­ское

10. 

Наибольшего значения

11. 

Наименьшего значения

12. 

Вейбулла-Гнеденко

 

 

 

2. Предельные распределения статистики Колмогорова

 

            На рис.1 приведены результаты моделирования величины , используемой в критерии Колмо­горова, при проверке гипотез о согласии с нормальным рас­пределением при справедливости гипотезы . На этом и последующих ри­сунках представлены эмпирические функции распреде­ле­ния статистики, когда по выборке не оценивались параметры (“1”), по выборке оценивался только масштабный параметр (“2”) (в данном случае ), оценивался только параметр сдвига (“3”) (в данном случае ), оценивались одновременно оба параметра (“4”). Здесь же приведена функ­ция распре­деления Колмогорова (“0”), которому подчиняется статистика , если по выборке не оцениваются параметры. Результаты проверки согласия эмпирического распределения “1” с распределением Колмогорова “0” доста­точно хорошее. В то же время весьма наглядно отличие эмпирических функций распре­деления “2”, “3”, “4” от распределения Колмогорова “0”. Это отличие позволяет судить о величине тех ошибок, которые мы допускаем, не учитывая факта оценивания пара­метров конкретного распределения при использовании критерия Колмого­рова. Крестиками, лежащими практи­чески на эмпирическом распределении “4”, обо­значены значения, соот­ветствующие процентным точкам при проверке нормальности, взятые из таблицы М. Стефенса [12], а кружочками - зна­чения, полученные по приближенным формулам Ю.Н. Тюрина [17,19] для расчетов вероятностей, соответствующих распре­делениям “4” и “2”.

 

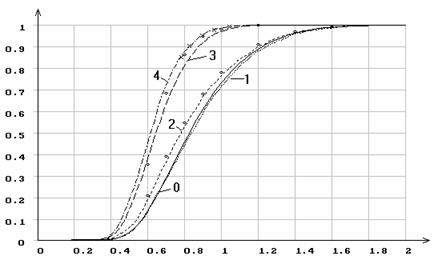
Рис.1. Эмпирические функции распределения статистики  Колмо­горова при различном количестве оцениваемых параметров нормального закона: 0 - функция распределения Колмогорова; 1 - по выборке не оценивались пара­метры; 2 - по выборке оценивался толь­ко масштабный параметр ; 3 - оце­нивался только параметр сдвига ; 4 - оце­нивались одновременно оба параметра.

Замечание: Процентные точки М.Стефенса соответствуют модифициро­ван­ной статис­тике вида , а по формулам Ю.Н.Тюрина рассчи­ты­вают вероятности для статистики . В то же время .

            Аналогичная картина распределения статистики Колмогорова при справедливой гипотезе  наблюдается для логистического распределения на рис. 2, для распределения Лапласа на рис. 3,  для распределения Коши на рис. 4 и для экспоненциального распределения на рис. 5, где крестиками, обо­значены значения, соот­ветствующие процентным точкам при проверке экспоненциальности и неизвестном масштабном параметре, взятые из таб­лицы процентных точек [12]. 

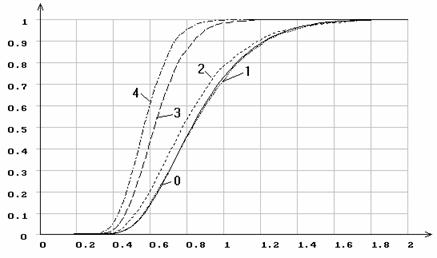
Рис.2. Эмпирические функции распределения статистики  Колмо­горова при различном количестве оцениваемых параметров логистического распределения

 

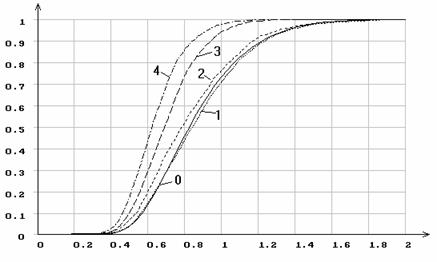
Рис.3. Эмпирические функции распределения статистики  Колмо­горова при различном количестве оцениваемых параметров распределения Лапласа

            Результаты моделирования однозначно указывают на то, что пре­дель­ные распре­деления статистики  при условии оценивания пара­метров конкретного закона настолько сильно отличаются от распределения Колмогорова, что исполь­зование последнего никак не может быть оправ­дано из-за высокого риска невер­ных выводов.

 

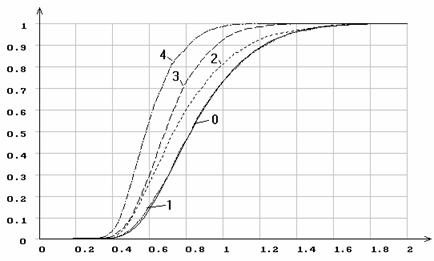
Рис.4. Эмпирические функции распределения статистики  Колмо­горова при различном количестве оцениваемых параметров распределения Коши

 

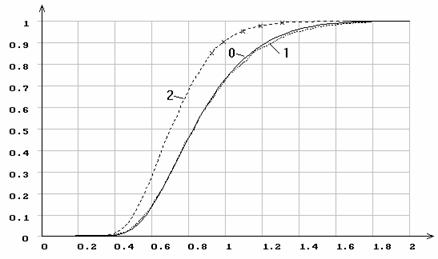
Рис.5. Эмпирические функции распределения статистики  Колмо­горова при различном количестве оцениваемых параметров экспонен­ци­аль­ного закона: 0 - функция распределения Колмогорова; 1 - по выборке не оценивались пара­метры; 2 - по выборке оценивался  масштабный параметр.

 

            При идентификации типов предельных законов распределения непа­ра­мет­рических ста­тистик в зависимости от вида закона наблюдаемой слу­чайной величины и количества оцениваемых по выборке параметров использовалось множество из 26 законов и семейств распреде­лений, вклю­ченных в программную систему [21]. Оказалось, что почти всегда эмпи­рические законы рас­пределе­ния ста­тистик непараметрических кри­териев наиболее хорошо описываются одним из двух законов распре­деления: логарифмически нормальным или гамма-распре­делением. То есть, эм­пи­ри­ческая функция статистики хорошо согласуется с одним из этих  законов по всем используемым в системе критериям согласия: отношения правдопо­добия,  Пирсона, Колмогорова, Смирнова,  и  Мизеса.

            На рис. 6 представлены результаты выравнивания распределения ста­тистики Колмогорова при оценивании одновременно двух параметров нормального распределения. На рисунке приведены эмпирическая фун­кция распределения статистики и функция распределения логарифмически нормального распределения с параметрами  (они практически совпали). Здесь же отражены значения статистик всех исполь­зуемых при проверке согласия критериев и соответствующие вероятности вида . Факт оцени­вания параметров логарифмически нормаль­ного распределения в крите­риях отношения правдо­по­добия и  Пирсона учитывается уменьшением числа степеней свободы -распределения. При­чем в критериях использовано асимптотически оптимальное группиро­ва­ние наблюдений при 15 интервалах, максимизирующее мощность при близ­ких альтернативах. Приведенные на рис. 6 значения вероятностей  для непа­ра­метрических статистик соответствуют классическим критериям (без учета факта оценивания пара­метров по данной выборке) и являются существенно завышенными. Если использовать представленные ниже в табл. 2, 5, 7, 9 результаты по аппроксимации смоделированных предельных распределений ста­тистик, то вероятность вида  для критерия Колмогорова соста­вит 0.6067, а не 0.8905, для кри­терия Смирнова - 0.4416, а не 0.5111, для критерия  Ми­зеса - 0.6277, а не 0.8897, для критерия  Мизеса - 0.4737, а не 0.8397.

            В табл. 2 сведены результаты идентификации законов для статистики критерия Колмогорова. Указание в клетке на конкретное распределение означает, что выборка со­от­ветству­ющей статистики хорошо описывается данным зако­ном (согла­су­ется с законом). В случае если согласие с каким-то законом не очень хорошее (гипотеза о согласии принимается с уровнем значимости ), то соот­вет­ствующий закон указан на сером фоне. В таблицах через  обо­значено логарифмически нормаль­ное рас­пре­деление с функ­цией плотности

,

 через  - гамма-распределение с функцией плотности

 .

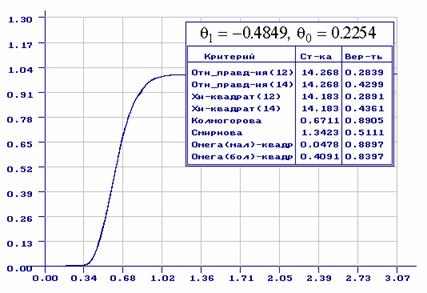
Рис.6. Эмпирическая функция распределения статистики Колмогорова при справедливой гипотезе  и оценивании 2-х параметров нормального распределения и выравнивающая её функция распределения логарифмически нормального распределения

 

Таблица 2.

Предельные распределения статистики Колмогорова

?

п/п

Распределение случайной величины

Оценивался только масштабный параметр

Оценивался только параметр сдвига

Оценивалось два параметра

1.     

Экспоненци­альное

lnN(-0.3477,0.2638)

 

 

2.     

Полунор­мальное

g(3.4090,8.2385,0.3443)

 

 

3.     

Рэлея

lnN(-0.3366,0.2579)

 

 

4.     

Максвелла

g(3.4809,9.0801,0.3417)

 

 

5.     

Лапласа

g(3.2121,6.5137,0.3400)

lnN(-0.3721,0.2426)

lnN(-0.4679,0.2329)

6.     

Нормальное

g(3.6448,7.0208,0.3164)

lnN(-0.4349,0.2337)

lnN(-0.4849,0.2254)

7.     

Логнормаль­ное

g(3.7326,7.4146,0.3265)

g(3.0857,8.4464,0.3532)

g(3.7311,10.045,0.3062)

8.     

Коши

g(3.1388,6.7500,0.3261)

lnN(-0.3691,0.2542)

g(4.2049,13.595,0.2983)

9.     

Логисти­че­ское

g(3.3283,6.6563,0.3280)

lnN(-0.4681,0.2248)

lnN(-0.5684,0.2111)

10. 

Наибольшего значения

g(3.5340,6.9273,0.3302)

lnN(-0.3588,0.2555)

lnN(-0.4950,0.2231)

11. 

Наименьшего значения

g(3.4746,6.9386,0.3362)

g(3.7737,9.3627,0.3293)

lnN(-0.5009,0.2221)

12. 

Вейбулла

g(3.6550,9.0285,0.3282)

lnN(-0.2325,0.2974) **

lnN(-0.5026,0.2202)

** - оценивался параметр формы распределения Вейбулла.

 

            Отметим, что предельные распределения статистики Колмогорова для выборок из распределения Вейбулла-Гнеденко, как это и доказано в [18], не зависят от параметров. В случае распределений экстремальных значений и распределения Вейбулла-Гнеденко могут использоваться одни и те же предельные распределения.

            Посмотрим, что будет получаться, если, например, мы будем исполь­зовать распределение Колмогорова для вычисления веро­ятности вида  в случае, когда по выборке предварительно вычис­ляются оценки параметров нормального распре­де­ле­ния. Распределение ста­тистики  в этом случае хорошо описывается логарифмически нормальным . Для сравнения в табл. 3 для неко­торых зна­чений статистик  представлены соответствующие значения функ­ции распре­де­ления Колмогорова, данного логарифмически нормального распре­де­ле­ния и эмпирической функции распределения , полученной при мо­де­­ли­ровании распределения статистики. Так, для распределения Колмо­горова величина , а для логарифмически нор­маль­ного . Это означает, что при значении ста­тистики , используя распределение Колмо­горова мы без­о­говорочно примем гипотезу , когда на самом деле даже при уровне значимости  она должна быть отклонена.

 

Таблица 3.

0.5

0.9

1.0

1.22

1.36

0.036055

0.607269

0.730000

0.898102

0.990154

0.177708

0.953880

0.984268

0.998791

0.999780

0.19

0.9533

0.98425

0.999

1

 

 

            Распределения, приводимые в табл. 2, удобны для реализации в про­граммном обеспечении задач статистического анализа, как это сделано в [21], так как для вычисления вероятностей вида , соответ­ству­ющих логарифмически нормальному или гамма-распределениям, не обой­тись без процедур численного интегрирования или использования прибли­женных формул. В то же время для большинства практиков, применяющих статистические методы в различных приложениях, более привычно опи­раться на верхние процентные точки распределений статистик. В табл. 4 приводятся приближенные значения верхних процентных точек для ста­тис­тики , которые для более высокой точности рассчитаны не по распределениям табл. 2, а получены сглаживанием “хвостов” эмпирических распределений. Точность этих про­центных точек вполне достаточна для корректного использования критерия в задачах статистического анализа.

 

 

Таблица 4.

 

Процентные точки распределения статистики Колмогорова

?

Распределение

Оцениваемые

Верхние процентные точки

п/п

случайной величины

параметры

0.15

0.1

0.05

0.025

0.01

1.

Экспоненци­альное

масштабный

0.9291

0.9872

1.0861

1.1846

1.3145

2.

Полунор­мальное

масштабный

0.9879

1.0519

1.1539

1.2511

1.3752

3.

Рэлея

масштабный

0.9402

0.9999

1.0952

1.1859

1.3017

4.

Максвелла

масштабный

0.9284

0.9890

1.0853

1.1770

1.2938

5.

Лапласа

масштабный

1.1081

1.1897

1.3222

1.4501

1.6147

 

 

сдвиг

0.8914

0.9435

1.0240

1.0992

1.1935

 

 

два параметра

0.7966

0.8467

0.9261

1.0016

1.0978

6.

Нормальное

масштабный

1.1208

1.2081

1.3446

1.4731

1.6356

 

 

сдвиг

0.8330

0.8790

0.9497

1.0156

1.0982

 

 

два параметра

0.7808

0.8255

0.8954

0.9611

1.0442

7.

Логнормаль­ное

масштабный

1.0880

1.1736

1.3147

1.4523

1.6308

 

 

сдвиг

0.9147

0.9875

1.1083

1.2266

1.3805

 

 

два параметра

0.8539

0.9268

1.0500

1.1723

1.3330

8.

Коши

масштабный

1.0590

1.1497

1.2950

1.4339

1.6116

 

 

сдвиг

0.9080

0.9659

1.0589

1.1481

1.2623

 

 

два параметра

0.7620

0.8117

0.8868

0.9557

1.0414

9.

Логисти­че­ское

масштабный

1.1034

1.1957

1.3441

1.4864

1.6689

 

 

сдвиг

0.7912

0.8373

0.9109

0.9813

1.0714

 

 

два параметра

0.7060

0.7400

0.7964

0.8516

0.9234

10.

Наибольшего

масштабный

1.1157

1.2033

1.3402

1.4689

1.6315

 

значения

сдвиг

0.9137

0.9775

1.0794

1.1765

1.3004

 

 

два параметра

0.7705

0.8119

0.8808

0.9485

1.0367

11.

Наименьшего

масштабный

1.1027

1.1897

1.3286

1.4612

1.6305

 

значения

сдвиг

0.9386

1.0048

1.1103

1.2108

1.3390

 

 

два параметра

0.7655

0.8080

0.8758

0.9405

1.0233

12.

Вейбулла

формы

1.0824

1.1659

1.3043

1.4396

1.6157

 

 

масштаба

0.9425

1.0064

1.1087

1.2065

1.3315

 

 

два параметра

0.7634

0.8022

0.8658

0.9276

1.0074

 

3. Предельные распределения статистики Смирнова

 

            На рис. 7 представлены результаты моделирования статистики Смир­нова  при справедливой гипотезе , соответствующей нормаль­ному рас­пределению, на рис. 8, соответствующей логистическому распреде­ле­нию, на рис. 9, соответствующей распределению Лапласа, на рис. 10. - распределению Коши, а на рис. 11 - экспоненциальному распределению. На этих рисунках символом “0” отмечена функция распределения , ко­то­рому подчиняется статистика Смирнова, если по выборке не оцениваются параметры.

 

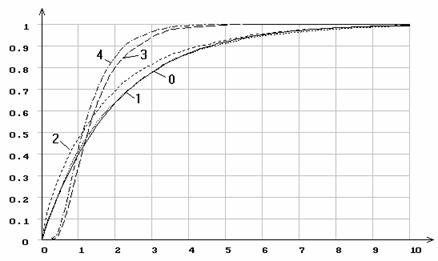
Рис.7. Эмпирические функции распределения статистики Смирнова при различном количестве оцениваемых параметров нормального закона: 0 - функция распределения  (с двумя степенями свободы); 1 - по выборке не оценивались параметры; 2 - по выборке оценивался только масштабный параметр ; 3 - оценивался только параметр сдвига ; 4 - оценивались одновременно оба параметра;

 

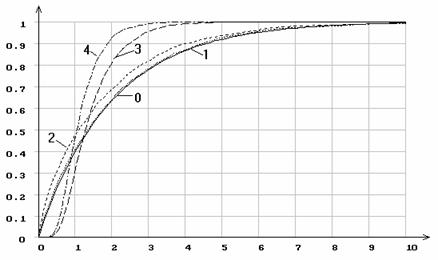
Рис.8. Эмпирические функции распределения статистики  Смирнова при различном количестве оцениваемых параметров логистического распре­де­ления

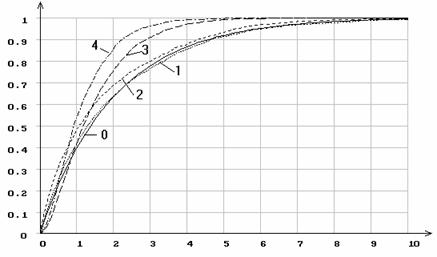
Рис.9. Эмпирические функции распределения статистики  Смирнова при различном количестве оцениваемых параметров распределения Лапласа

 

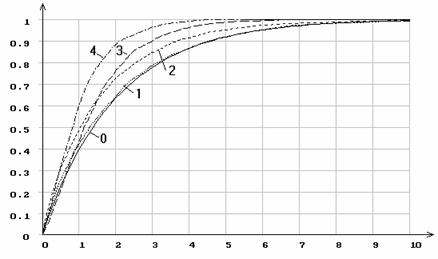
Рис.10. Эмпирические функции распределения статистики  Смирнова при различном количестве оцениваемых параметров распределения Коши

 

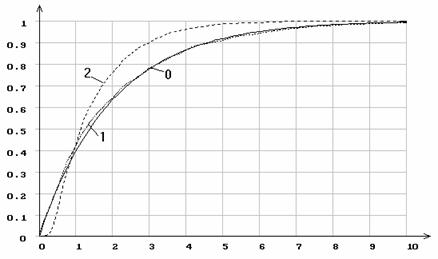
Рис.11. Эмпирические функции распределения статистики  Смирнова без оценивания параметров (1), при оценивании масштабного параметра (2) экспонен­циального распределения

 

            Как видим, и в данном случае предельные распре­деления статистики Смирнова при условии оценивания параметров конкретного закона карди­нально отличаются от распределения .

            Выше уже говорилось, что о точности моделирования можно су­дить по результатам моделирования классических непара­метри­чес­ких статистик (без оценивания параметров). На рис. 12 для иллюстрации приведены результаты проверки гипотез о согласии с -распределе­нием смоде­ли­ро­ванной выборки классической статистики Смирнова в случае нормального закона (см. рис. 7). На рисунке отражены функция плотности -распре­деления и гистограмма, построенная по выборке при асимптотически опти­мальном группировании.

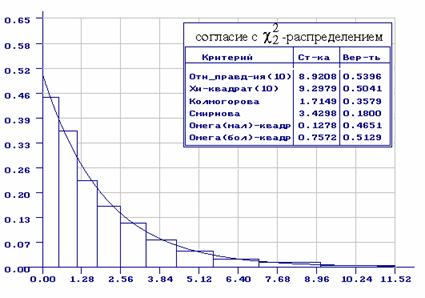
Рис.12. Результаты статистического анализа смоделированной выборки клас­сической статистики Смирнова (для нормального закона без оцени­вания параметров)

 

            В табл. 5 сведены результаты идентификации предельных законов для статистики критерия Смирнова.

 

Таблица 5.

Предельные распределения статистики Смирнова

?

п/п

Распределение случайной величины

Оценивался только масштабный параметр

Оценивался только параметр сдвига

Оценивалось два параметра

1.     

Экспоненци­альное

lnN(0.1585,0.7009)

 

 

2.     

Полунор­мальное

lnN(0.1289,0.7900)

 

 

3.     

Рэлея

lnN(0.1936,0.7073)

 

 

4.     

Максвелла

lnN(0.2221,0.6794)

 

 

5.     

Лапласа

g(0.8146,0.4654,0.0006)

g(1.7664,1.2256,0.0207)

g(1.8235,1.5842,0.0058)

6.     

Нормальное

g(0.8088,0.4549,0.0006)

lnN(0.2471,0.5321)

lnN(0.1299,0.5331)

7.     

Логнормаль­ное

g(0.8391,0.4641,0.0006)

lnN(0.4252,0.6481)

lnN(0.1947,0.6783)

8.     

Коши

g(0.8570,0.5348,0.0006)

g(1.4215,0.9846,0.0006)

g(1.2931,1.2542,0.0006)

9.     

Логисти­че­ское

g(0.8164,0.4709,0.0)

lnN(0.2684,0.4856)

lnN(0.0569,0.4491)

10. 

Наибольшего значения

g(0.8507,0.4682,0.0006)

lnN(0.2667,0.6821)

lnN(0.1049,0.5058)

11. 

Наименьшего значения

g(0.8234,0.4592,0.0006)

lnN(0.2022,0.7015)

lnN(0.1238,0.5024)

12. 

Вейбулла

lnN(0.1615,0.7186)

g(0.8641,0.4851,0.0006)**

g(2.3495,2.3008,0.2564)

** - оценивался параметр формы распределения Вейбулла.

 

            В табл. 6 приводятся приближенные значения верхних процентных точек для ста­тис­тики .

 

Таблица 6.

 Процентные точки распределения статистики Смирнова

?

Распределение

Оцениваемые

Верхние процентные точки

п/п

случайной величины

параметры

0.15

0.1

0.05

0.025

0.01

1.

Экспоненци­альное

масштабный

2.5341

2.9847

3.7675

4.5593

5.6145

2.

Полунор­мальное

масштабный

2.6856

3.2651

4.2439

5.2147

6.4902

3.

Рэлея

масштабный

2.6590

3.1390

3.9317

4.7058

5.7115

4.

Максвелла

масштабный

2.5751

3.0644

3.9162

4.7788

5.9296

5.

Лапласа

масштабный

3.5933

4.3253

5.5464

6.7473

8.3154

 

 

сдвиг

2.5139

2.9110

3.5728

4.2230

5.0716

 

 

два параметра

1.9821

2.2836

2.8034

3.3261

4.0201

6.

Нормальное

масштабный

3.4951

4.3824

5.8586

7.3074

9.1966

 

 

сдвиг

2.2762

2.6147

3.1684

3.7055

4.3998

 

 

два параметра

2.0255

2.3001

2.7552

3.2005

3.7801

7.

Логнормаль­ное

масштабный

3.4308

4.2549

5.6948

7.1566

9.1105

 

 

сдвиг

3.0417

3.6974

4.8495

6.0236

7.5972

 

 

два параметра

2.3621

2.9020

3.9162

4.9983

6.4985

8.

Коши

масштабный

3.0648

3.7974

5.0833

6.3929

8.1473

 

 

сдвиг

2.5211

2.9562

3.7225

4.5046

5.5542

 

 

два параметра

1.8510

2.1830

2.7286

3.2596

3.9478

9.

Логисти­че­ское

масштабный

3.3625

4.1502

5.5238

6.9163

8.7754

 

 

сдвиг

2.1914

2.4814

2.9781

3.4754

4.1334

 

 

два параметра

1.6973

1.9035

2.2459

2.5814

3.0185

10.

Наибольшего

масштабный

3.5767

4.3936

5.7430

7.0609

8.7735

 

значения

сдвиг

2.6771

3.1331

3.9274

4.7318

5.8051

 

 

два параметра

1.8947

2.1702

2.6283

3.0778

3.6638

11.

Наименьшего

масштабный

3.5733

4.3186

5.5688

6.8028

8.4186

 

значения

сдвиг

2.6298

3.1309

3.9946

4.8630

6.0157

 

 

два параметра

1.9043

2.1615

2.6199

3.0917

3.7285

12.

Вейбулла

формы

3.4390

4.1895

5.5179

6.8786

8.7090

 

 

масштаба

2.5623

3.0621

3.9347

4.8203

6.0035

 

 

два параметра

1.9035

2.1477

2.5708

2.9977

3.5659

 

 

4. Предельные распределения статистики Крамера-Мизеса-Смирнова

 

            Результаты моделирования статистики  Мизеса (Крамера-Мизеса-Смирнова) при спра­ведливой гипотезе  для случая нормального рас­пре­деления представлены на рис. 13. На этом рисунке крестиками нанесены соответствующие значения пре­дель­ных распределений, полученные в ра­бо­те Г.В. Мартынова [7]. Для случая логистического распре­деления ре­зуль­таты моделиро­вания приведены на рис. 14, для случая рас­пределения Лапласа - на рис. 15, для распределения Коши - на рис. 16, а на рис. 17 - для экс­поненциального распределения, где для сравнения крести­ками обозна­чены процентные точки при проверке экспонен­ци­аль­ности из таблицы М.Сте­фенса [12]. На этих рисунках символом “0” отмечена функция рас­пре­де­ления  [22], предельная для этой статистики, если по выборке не оце­ни­вались параметры распределения.

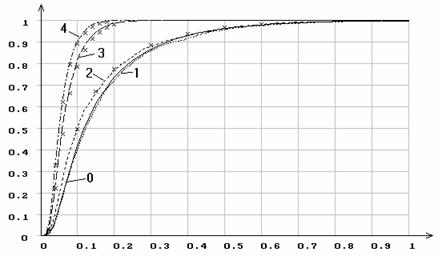
Рис.13. Эмпирические функции распределения статистики  Мизеса при различном количестве оцениваемых параметров нормального закона: 0 - функция распределения ; 1 - по выборке не оценивались параметры; 2 - по выборке оценивался только масштабный параметр ; 3 - оценивался только параметр сдвига ; 4 - оценивались одновременно оба параметра.

 

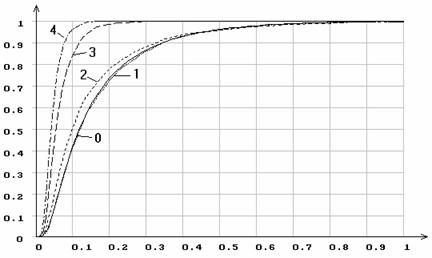
Рис.14. Эмпирические функции распределения статистики  Мизеса при различном количестве оцениваемых параметров логистического распре­деления

 

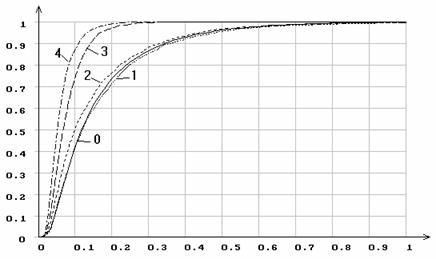
Рис.15. Эмпирические функции распределения статистики  Мизеса при различном количестве оцениваемых параметров распределения Лапласа

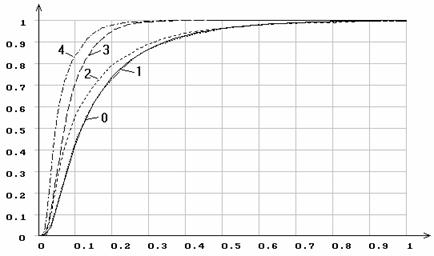
Рис.16. Эмпирические функции распределения статистики  Мизеса при различном количестве оцениваемых параметров распределения Коши

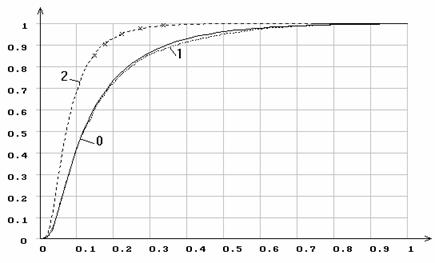
Рис.17. Эмпирические функции распределения статистики  Мизеса при различном количестве оцениваемых параметров экспоненциального распре­деления

            В табл. 7 сведены результаты идентификации законов для статистики критерия  Ми­зеса. Следует отметить, что в данном случае предельные распределения хуже аппроксимируются логарифмически нормальным, ко­торое в каждом случае оказалось наиболее подходящим из всего множества законов, включенных в систему [21].

 

Таблица 7.

Предельные распределения статистики Мизеса

?

п/п

Распределение случайной величины

Оценивался только масштабный параметр

Оценивался только параметр сдвига

Оценивалось два параметра

1.     

Экспоненци­альное

lnN(-2.6028,0.6453)

 

 

2.     

Полунор­мальное

lnN(-2.5046,0.6814)

 

 

3.     

Рэлея

lnN(-2.5743,0.6345)

 

 

4.     

Максвелла

lnN(-2.6147,0.6361)

 

 

5.     

Лапласа

lnN(-2.2328,0.8302)

lnN(-2.6890,0.5802)

lnN(-2.9386,0.5500)

6.     

Нормальное

lnN(-2.2290,0.8284)

lnN(-2.8102,0.5625)

lnN(-2.9685,0.5187)

7.     

Логнормаль­ное

lnN(-2.2334,0.7951)

lnN(-2.6226,0.6972)

lnN(-2.8233,0.6673)

8.     

Коши

lnN(-2.3228,0.8554)

lnN(-2.6269,0.6202)

lnN(-2.9746,0.6493)

9.     

Логисти­че­ское

lnN(-2.2460,0.8329)

lnN(-2.8755,0.5612)

lnN(-3.1713,0.4841)

10. 

Наибольшего значения

lnN(-2.2043,0.8174)

lnN(-2.6070,0.6178)

lnN(-3.0093,0.5078)

11. 

Наименьшего значения

lnN(-2.2246,0.8149)

lnN(-2.5863,0.6469)

lnN(-3.0200,0.5173)

12. 

Вейбулла

lnN(-2.5875,0.6669)

lnN(-2.2404,0.7910) **

lnN(-3.0258,0.5058)

** - оценивался параметр формы распределения Вейбулла.

 

            В табл. 8 представлены полученные приближенные значения верхних процентных точек для ста­тис­тики .

 

Таблица 8.

 Процентные точки распределения статистики  Мизеса

?

Распределение

Оцениваемые

Верхние процентные точки

п/п

случайной величины

параметры

0.15

0.1

0.05

0.025

0.01

1.

Экспоненци­альное

масштабный

0.1463

0.1752

0.2263

0.2785

0.3486

2.

Полунор­мальное

масштабный

0.1730

0.2073

0.2673

0.3283

0.4098

3.

Рэлея

масштабный

0.1518

0.1790

0.2253

0.2713

0.3319

4.

Максвелла

масштабный

0.1463

0.1738

0.2208

0.2681

0.3306

5.

Лапласа

масштабный

0.2702

0.3394

0.4594

0.5809

0.7427

 

 

сдвиг

0.1249

0.1440

0.1770

0.2103

0.2546

 

 

два параметра

0.0942

0.1103

0.1377

0.1651

0.2014

6.

Нормальное

масштабный

0.2711

0.3414

0.4636

0.5871

0.7515

 

 

сдвиг

0.1096

0.1270

0.1561

0.1847

0.2222

 

 

два параметра

0.0874

0.0998

0.1208

0.1417

0.1691

7.

Логнормаль­ное

масштабный

0.2599

0.3235

0.4347

0.5476

0.6987

 

 

сдвиг

0.1481

0.1902

0.2709

0.3580

0.4799

 

 

два параметра

0.1134

0.1474

0.2154

0.2912

0.3996

8.

Коши

масштабный

0.2565

0.3278

0.4545

0.5848

0.7604

 

 

сдвиг

0.1416

0.1656

0.2060

0.2461

0.2987

 

 

два параметра

0.1062

0.1285

0.1660

0.2031

0.2518

9.

Логисти­че­ское

масштабный

0.2648

0.3369

0.4667

0.6012

0.7838

 

 

сдвиг

0.1027

0.1200

0.1507

0.1822

0.2245

 

 

два параметра

0.0692

0.0784

0.0943

0.1161

0.1354

10.

Наибольшего

масштабный

0.2752

0.3413

0.4601

0.5829

0.7494

 

значения

сдвиг

0.1435

0.1697

0.2133

0.2560

0.3117

 

 

два параметра

0.0840

0.0963

0.1172

0.1380

0.1654

11.

Наименьшего

масштабный

0.2649

0.3324

0.4541

0.5804

0.7518

 

значения

сдвиг

0.1500

0.1774

0.2269

0.2785

0.3488

 

 

два параметра

0.0848

0.0974

0.1182

0.1383

0.1644

12.

Вейбулла

формы

0.2521

0.3165

0.4292

0.5438

0.6971

 

 

масштаба

0.1535

0.1855

0.2405

0.2956

0.3686

 

 

два параметра

0.0833

0.0940

0.1125

0.1311

0.1557

 

 

5. Предельные распределения статистики Андерсона-Дарлинга

 

            На рис. 18-22 отражены резуль­таты моделиро­ва­ния предельных зако­нов распределения статистики  Мизеса (Андерсона-Дарлинга). На ри­сунках символом “0” отмечена функция распределения  [18]. Этому распределению подчиняется статистика , если по выборке не оцени­ва­ются параметры наблюдаемого закона.

 

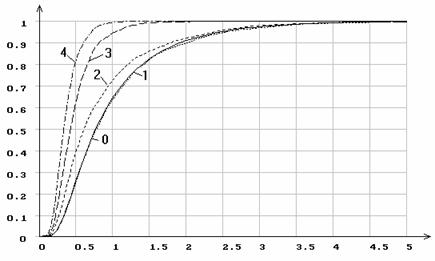
Рис. 18. Эмпирические функции распределения статистики  Мизеса при различном количестве оцениваемых параметров нормального закона: 0 - функция распределения ; 1 - по выборке не оценивались параметры; 2 - по выборке оценивался только масштабный параметр ; 3 - оценивался только параметр сдвига ; 4 - оценивались одновременно оба параметра.

 

 

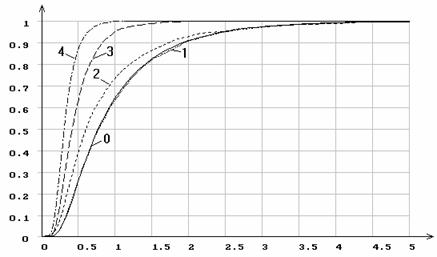
Рис.19. Эмпирические функции распределения статистики  Мизеса при различном количестве оцениваемых параметров логистического распре­деления

 

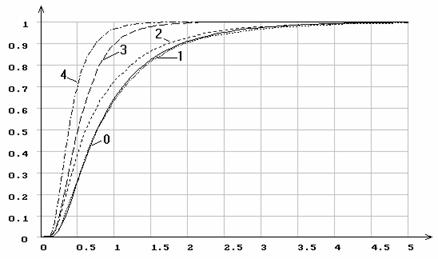
Рис.20. Эмпирические функции распределения статистики  Мизеса при различном количестве оцениваемых параметров распределения Лапласа

 

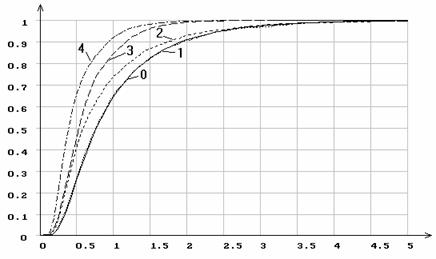
Рис.21. Эмпирические функции распределения статистики  Мизеса при различном количестве оцениваемых параметров распределения Коши

 

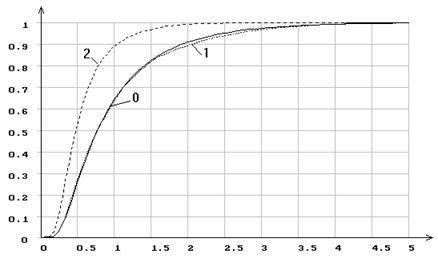
Рис.22. Эмпирические функции распределения статистики  Мизеса при различном количестве оцениваемых параметров экспоненциального распре­деления

 

            В табл. 9 сведены результаты идентификации законов для статистики критерия  Ми­зеса. Как и в предыдущем случае здесь предельные рас­пределения также хуже аппроксимируются логариф­мически нормаль­ным распределением.

 

Таблица 9.

Предельные распределения статистики Мизеса

?

п/п

Распределение случайной величины

Оценивался только масштабный параметр

Оценивался только параметр сдвига

Оценивалось два параметра

1.     

Экспоненци­альное

lnN(-0.7055,0.5690)

 

 

2.     

Полунор­мальное

lnN(-0.6931,0.5900)

 

 

3.     

Рэлея

lnN(-0.6850,0.5541)

 

 

4.     

Максвелла

lnN(-0.7051,0.5658)

 

 

5.     

Лапласа

lnN(-0.4107,0.7170)

lnN(-0.6654,0.5345)

lnN(-0.9378,0.4999)

6.     

Нормальное

lnN(-0.4121,0.7206)

lnN(-0.8363,0.5096)

lnN(-1.0840,0.4509)

7.     

Логнормаль­ное

lnN(-0.4092,0.6938)

lnN(-0.6827,0.6146)

lnN(-0.9322,0.5819)

8.     

Коши

lnN(-0.4326,0.7164)

lnN(-0.6102,0.5737)

lnN(-0.8815,0.5905)

9.     

Логисти­че­ское

lnN(-0.4243,0.7224)

lnN(-0.8465,0.5109)

lnN(-1.1685,0.4239)

10. 

Наибольшего значения

lnN(-0.3863,0.7097)

lnN(-0.6903,0.5534)

lnN(-1.0809,0.4447)

11. 

Наименьшего значения

lnN(-0.4007,0.7108)

lnN(-0.6866,0.5667)

lnN(-1.0986,0.4474)

12. 

Вейбулла

lnN(-0.6908,0.5866)

lnN(-0.4177,0.6846) **

lnN(-1.1044,0.4405)

** - оценивался параметр формы распределения Вейбулла.

 

            В табл. 10 приведены приближенные значения верхних процентных точек для ста­тис­тики .

 

Таблица 10.

 

Процентные точки распределения статистики  Мизеса

?

Распределение

Оцениваемые

Верхние процентные точки

п/п

случайной величины

параметры

0.15

0.1

0.05

0.025

0.01

1.

Экспоненци­альное

масштабный

0.8975

1.0599

1.3407

1.6235

1.9995

2.

Полунор­мальное

масштабный

0.9912

1.1672

1.4791

1.7987

2.2289

3.

Рэлея

масштабный

0.9168

1.0629

1.3128

1.5629

1.8938

4.

Максвелла

масштабный

0.8975

1.0569

1.3342

1.6150

1.9896

5.

Лапласа

масштабный

1.4505

1.7830

2.3789

2.9943

3.8275

 

 

сдвиг

0.8979

1.0326

1.2598

1.4851

1.7810

 

 

два параметра

0.6604

0.7593

0.9312

1.1051

1.3369

6.

Нормальное

масштабный

1.4538

1.8026

2.4220

3.0579

3.9146

 

 

сдвиг

0.7300

0.8371

1.0340

1.2410

1.5249

 

 

два параметра

0.5409

0.6095

0.7239

0.8366

0.9837

7.

Логнормаль­ное

масштабный

1.4278

1.7433

2.2896

2.8407

3.5739

 

 

сдвиг

0.9489

1.1734

1.5913

2.0342

2.6453

 

 

два параметра

0.6893

0.8589

1.2006

1.5829

2.1318

8.

Коши

масштабный

1.4282

1.7664

2.3817

3.0238

3.8996

 

 

сдвиг

1.0213

1.1849

1.4549

1.7185

2.0607

 

 

два параметра

0.8019

0.9480

1.1928

1.4345

1.7508

9.

Логисти­че­ское

масштабный

1.4373

1.7879

2.4150

3.0617

3.9361

 

 

сдвиг

0.7344

0.8489

1.0486

1.2510

1.5213

 

 

два параметра

0.4849

0.5423

0.6364

0.7277

0.8460

10.

Наибольшего

масштабный

1.4936

1.8259

2.4120

3.0108

3.8148

 

значения

сдвиг

0.9061

1.0523

1.3054

1.5607

1.9004

 

 

два параметра

0.5443

0.6107

0.7248

0.8392

0.9907

11.

Наименьшего

масштабный

1.4538

1.7934

2.3948

3.0111

3.8404

 

значения

сдвиг

0.9088

1.0660

1.3426

1.6250

2.0039

 

 

два параметра

0.5398

0.6092

0.7198

0.8251

0.9594

12.

Вейбулла

формы

1.3909

1.7030

2.2511

2.8096

3.5579

 

 

масштаба

0.9355

1.1049

1.4018

1.7039

2.1081

 

 

два параметра

0.5253

0.5908

0.6991

0.8052

0.9432

 

 

6. Предельные распределения статистик для выборок из гамма-распределения

 

            Как и следовало ожидать, предельные распределения рассма­три­ва­емых статистик для выборок из гамма-распределения с плотностью

зависят от параметра формы . Выборки статистик моделировались при различных значениях параметра . Для иллюстрации мы приведем лишь результаты моделирования статистики Колмогорова . На рис. 23 пред­ставлены эмпирические распределения статистики при оценивании по выборке параметра формы, на рис. 24 - масштабного пара­метра, на рис. 25 - двух параметров распределения. На этих рисунках “1” помечена эмпи­рическая функция распределения статистики при =0.5; “2” - при =1.0; “3” - при =2.0; “4” - при =5.0; “5” - при =10.0. “0” помечена функция распределения Колмогорова. Отметим, что с ростом  пре­дель­ные распре­деления статистик стремятся к предельным распределениям ста­тис­тик для выборок из нор­мального закона. При значениях >5 эмпи­рические распределения статис­тик при оценива­нии двух параметров прак­ти­чески совпадают и хорошо согласуются с распре­делением соответ­ству­ющей статистики для нормаль­ного закона.

            Общая картина принципиально со­хра­няется и для распределений других непараметрических статистик.

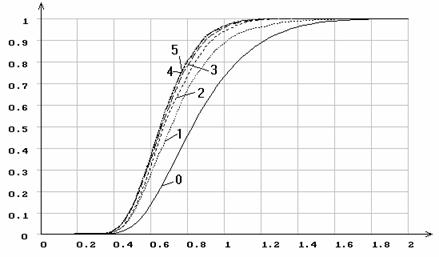
Рис.23. Эмпирические функции распределения статистики  Колмо­горова при оценивании параметра формы гамма-рапределения: 0 - функция распределения Колмогорова; 1 - =0.5; 2 - =1.0; 3 - =2.0; 4 - =5.0; 5 - =10.0.

 

7. Заключение

 

            Можно констатировать, что на основании результатов модели­ро­ва­ния могут быть получены хорошие приближения предельных распреде­лений непараметрических статистик.

            Для законов, определяемых только параметрами сдвига и масштаба наи­более значительное влияние на предельные распределения всех непара­метрических статистик оказывает оценивание параметра сдвига, в сущес­твенно меньшей степени - оценивание масштабного параметра.

            Достаточно хорошая аппроксимация для реальных распределений ста­тис­тик непараметрических критериев обычно может быть получена с использо­ва­нием логарифмически нормального распределения и/или гам­ма-распре­деления. Для ряда законов распределения случайных величин иден­ти­фицированы законы распре­де­ления статистик непараметричеких крите­риев при раз­личном количестве оце­ненных параметров, построены таб­лицы верхних процентных точек. Полученные рас­пределения при прак­ти­ческом использовании критериев согласия позво­лят делать более надежные статистические выводы.

 

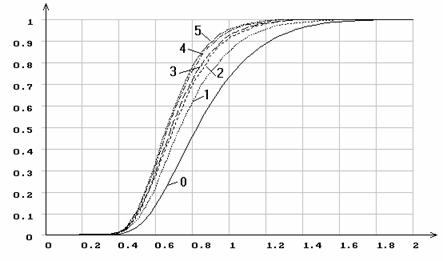
Рис.24. Эмпирические функции распределения статистики  Колмо­горова при оценивании масштабного параметра гамма-рапределения: 0 - функция распределения Колмогорова; 1 - =0.5; 2 - =1.0; 3 - =2.0; 4 - =5.0; 5 - =10.0.

 

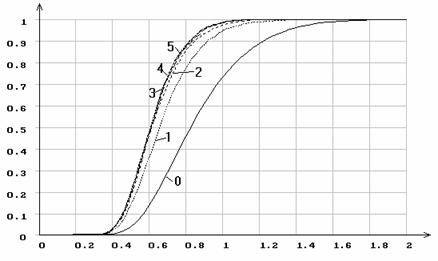
Рис.25. Эмпирические функции распределения статистики  Колмо­горова при оценивании одновременно двух параметров гамма-рапределения: 0 - функция распределения Колмогорова; 1 - =0.5; 2 - =1.0; 3 - =2.0; 4 - =5.0; 5 - =10.0.

 

 

            В случае необходимости, вообще говоря, несложно провести анало­гич­ное моделирование распре­делений статис­тик непараметрических крите­риев для любого закона распределения случайной величины.

            Результаты проведенных исследований еще раз подчеркивают, что предельные распределения статистик непараметрических критериев со­гла­сия Колмого­рова, Смирнова,  и  Ми­зеса при оценивании по вы­борке параметров в случае справедли­вости гипотезы  настолько силь­но от­личаются от распределений классических статистик, соответственно зако­нов , ,  и , что по­следние ни в коем случае не должны использоваться в такой ситуации.

 

Литература

 

1.       Kac M., Kiefer J., Wolfowitz J. On tests of normality and other tests of goodness of fit based on distance methods // Ann. Math. Stat., 1955. V.26. - P.189-211.

2.       Орлов А.И. Распространенная ошибка при использовании критериев Колмогорова и омега-квадрат // Заводская лаборатория, 1985. Т. 51. №1. - С. 60-62.

3.       Бондарев Б.В.  О проверке сложных статистических гипотез // Заводская лаборатория. 1986. Т. 52. № 10. - С. 62-63.

4.       Кулинская Е.В., Саввушкина Н.Е. О некоторых ошибках в реализации и применении непараметрических методов в пакете для IBM PC // Заводская лаборатория, 1990. Т. 56. № 5. - С. 96-99.

5.       Durbin J. Kolmogorov-Smirnov tests when parameters are estimated // Lect. Notes Math., 1976. V.566. - P.33-44.

6.       Никитин Я.Ю. Асимптотическая эффективность непараметрических кри­териев. - М.: Физматлит. 1995. - 240 с.

7.       Мартынов Г.В. Критерии омега-квадрат. - М.: Наука, 1978. - 80 с.

8.       Birnbaum Z.W. Numerical tabulation of the distribution of Kolmogoroff`s statistic for finite sample size // J. Am. Statist. Assoc., 1952. V.47. - P.425-441.

9.       Anderson T.W., Darling D.A. Asymptotic theory of certain ‘goodness of fit’ criteria based on stochastic processes // Ann. Math. Stat., 1952. V.23. - P.193-212.

10.   Lilliefors H.W. On the Kolmogorov-Smirnov test for normality with mean and variance unknown // J. Am. Statist. Assoc., 1967. V.62. - P.399-402.

11.   Lilliefors H.W. On the Kolmogorov-Smirnov test for the exponential distribution with mean unknown // J. Am. Statist. Assoc., 1969. V.64. - P.387-389.

12.   Pearson E.S., Hartley H.O. Biometrika tables for Statisticians. Vol. 2. - Cambridge: University Press. 1972. - 634 p.

13.   Stephens M.A. Use of Kolmogorov - Smirnov, Cramer - von Mises and related statistics - without extensive tables // J. R. Stat. Soc., 1970. B.32. - P.115-122.

14.   Stephens M.A. EDF statistics for goodness of fit and some comparisons // J. Am. Statist. Assoc., 1974. V.69. - P.730-737.

15.   Chandra M., Singpurwalla N.D., Stephens M.A. Statistics for Test of Fit for the Extreme-Value and Weibull Distribution // J. Am. Statist. Assoc., 1981. V.76. - P.375.

16.   Durbin J. Kolmogorov-Smirnov tests when parameters are estimated with applications to tests of exponentially and tests of spacings // Biometrika, 1975. V.62, № 1. - P.5-22.

17.   Тюрин Ю.Н. О предельном распределении статистик Колмогорова-Смирнова для сложной гипотезы / Известия АН СССР. Сер. Матем. 1984. Т. 48. № 6. - С. 1314-1343.

18.   Тюрин Ю.Н., Саввушкина Н.Е. Критерий согласия для распределения Вейбулла-Гнеденко / Известия АН СССР. Сер. Техн. ки­бернетика. 1984. № 3. - С. 109-112.

19.   Тюрин Ю.Н. Исследования по непараметрической статистике (непара­метрические методы и линейная модель). Автореф. дисс. докт. физ.-мат. наук. - М.: МГУ, 1985. - 33 с.

20.   Тюрин Ю.Н., Макаров А.А. Анализ данных на компьютере. - М.: ИНФРА-М, Финансы и статистика, 1995. - 384 с.

21.   Лемешко Б.Ю. Статистический анализ одномерных наблюдений слу­чай­ных величин: Программная система. - Новоси­бирск: Изд-во НГТУ. - 1995. - 125 с.

22.   Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. - М.: Наука, 1983. - 416 с.

 

 

[Содержание]