См. также: Прикладная математическая статистика (материалы к семинарам)

Заводская лаборатория. 1998. Т. 64. - № 5. - С.56-63.

УДК 519.2

О зависимости предельных распределений статистик хи-квадрат Пирсона и отношения правдоподобия от способа группирования данных

Б.Ю. Лемешко, С.Н. Постовалов

            В критериях согласия  Пирсона и отношения правдоподобия при вычислении соответствующих им статистик осуществляют группирование наблюдений. Неоспоримо, что вычисленные по конкретной выборке значения рассматриваемых статистик очень сильно зависят от того, как сгруппированы данные: выбрали интервалы группирования одним способом – нулевая гипотеза  о согласии должна быть отвергнута, другим – нет оснований её отвергать. Очевидно, что предельные распределения статистик критериев  Пирсона и отношения правдоподобия зависят не только от числа оцененных параметров, но и от способа группирования, вида исследуемого закона распределения , метода оценивания и типа оцениваемого параметра.

            Статистика  Пирсона вычисляется в соответствии с соотношением

,                                    (1)

где  – количество наблюдений, попавших в интервал,  - вероятность попадания наблюдения в -й интервал. При справедливой гипотезе  ее предельное распределение  есть -распределение с числом степеней свободы . Если по выборке оценивалось  параметров закона в результате минимизации статистики , статистика подчиняется -распределению с  степеней свободы. При справедливой альтернативной гипотезе  предельное распределение  представляет собой нецентральное -распределение с тем же числом степеней свободы и параметром нецентральности

.

            В случае проверки сложных гипотез и оценивании по выборке параметров распределений использование в качестве предельных -распределений справедливо лишь при определении оценок параметров по сгруппированным данным [1] и использовании для оценивания статистики . При вычислении оценок максимального правдоподобия по негруппированным данным эта статистика распределена в пределе как сумма независимых слагаемых , где  - стандартные нормальные случайные величины, независимые между собой и с , а  - некоторые числа между 0 и 1 [2-4]. И ее функция распределения лежит между - и - распределениями. Гипотеза о согласии не должна отвергаться, если

,

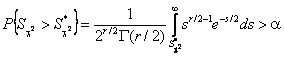где  - задаваемый уровень значимости.

            В критерии отношения правдоподобия статистика имеет вид [1]

.

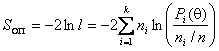При верной гипотезе  эта статистика асимптотически распределена так же, как и статистика  Пирсона.

-распределения используются в качестве предельных для статистик  Пирсона и отношения правдоподобия независимо от того, каким образом сгруппированы данные в интервалы.

            При практическом использовании критериев согласия выбирают либо интервалы равной длины, либо интервалы равной вероятности (равной частоты), либо асимптотически оптимальные интервалы (в этом случае минимизируются потери в информации Фишера) [5]. Использование интервалов равной вероятности было предложено ещё в работе [6]. Разбиение области определения случайной величины (размаха выборки) на интервалы равной длины неоднозначно. Более определенными способами являются равновероятное и асимптотически оптимальное группирование. При асимптотически оптимальном группировании мощность этих критериев для близких альтернатив максимальна [5]. Наш опыт применения данных критериев согласия показывает, что при использовании равновероятного группирования и малых отклонениях выборки от предположений значения статистик существенно меньше, а вероятности “согласия” вида , где  - значение статистики, вычисленное по выборке, значительно выше, чем при асимптотически оптимальном. При асимптотически оптимальном группировании лучше улавливаются небольшие отклонения выборки от предположений.

            Очевидно, что выбор равновероятного или асимптотически оптимального группирования отражается на предельных распределениях статистик  при верной альтернативной гипотезе. При использовании асимптотически оптимального группирования распределения  и  максимально “сдвинуты” относительно друг друга [5]. Надо полагать, что распределение статистики  при справедливой нулевой гипотезе также зависит от способа группирования.

            Если значения одной и той же статистики так сильно отличаются при различных способах группирования, то можем ли мы при практическом использовании критерия согласия использовать один и тот же предельный закон? Насколько сильно законы распределения статистик отличаются от соответствующего -распределения, особенно при определении оценок по негруппированным данным? Если действительная функция распределения статистики проходит выше используемого предельного теоретического , при проверке согласия увеличивается вероятность ошибок второго рода (принятие гипотезы при справедливой ), ниже – вероятность ошибок первого рода (отклонения верной гипотезы ).

            Целью данной работы явилось желание выяснить, насколько сильно отличаются предельные распределения рассматриваемых статистик при равновероятном и асимптотически оптимальном группировании (при справедливости гипотезы ) в зависимости от того, с каким законом проверяется согласие, сколько параметров оценивалось по выборке, каким образом они оценивались, а также предложить соответствующие рекомендации для практики статистического анализа.

            Для этого моделировались и исследовались эмпирические законы распределений статистик критериев  Пирсона и отношения правдоподобия, вычисляемых при равновероятном и асимптотически оптимальном группировании.

            По каждому закону распределения  моделировалась серия из  выборок объемом . По каждой выборке оценивались параметры этого закона распределения (один параметр, или другой, или два одновременно). Затем вычислялись значения статистик критериев  Пирсона и отношения правдоподобия при равновероятном и асимптотически оптимальном группировании. По накопленной выборке значений статистики объема  анализировалось полученное эмпирическое распределение статистики и осуществлялась идентификация закона. Оценки параметров находились по методу максимального правдоподобия по негруппированным данным.

            В соответствии с изложенным алгоритмом моделировались выборки значений статистик , . Далее мы приводим результаты моделирования и анализа, которые вместе с результатами, изложенными в [7], позволяют сделать определенные выводы.

            На приводимых ниже рисунках с результатами моделирования эмпирических распределений статистик “1” отмечено распределение статистики при асимптотически оптимальном группировании, а “2” - при равновероятном группировании. На рис. 1-3 представлены распределения статистики  при 5 интервалах группирования и оценивании параметров нормального распределения. На рис. 4-6 - распределения статистики  при оценивании параметров распределения наибольшего значения.

            Для сравнения на рис. 7 представлены распределения статистики  при 5 интервалах группирования и оценивании обоих параметров нормального распределения при асимптотически оптимальном и равновероятном группировании.

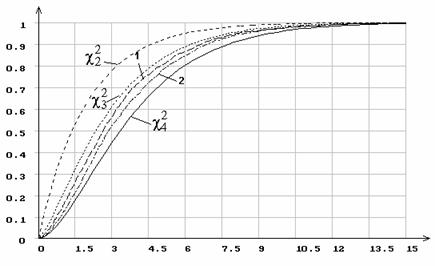
Рис. 1. Распределение статистики при 5 интервалах группирования

и оценивании масштабного параметра нормального распределения.

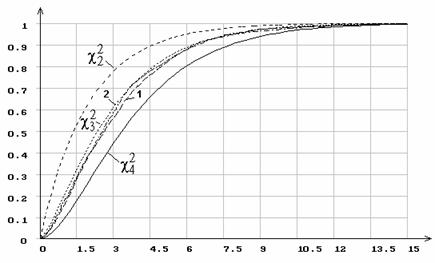
Рис. 2. Распределение статистики при 5 интервалах группирования

и оценивании параметра сдвига нормального распределения.

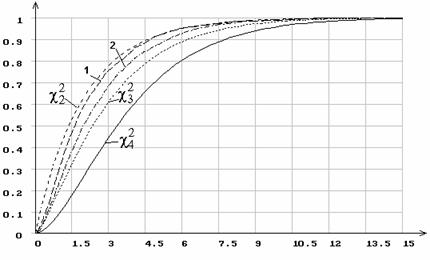
Рис. 3. Распределение статистики при 5 интервалах группирования

и оценивании двух параметров нормального распределения.

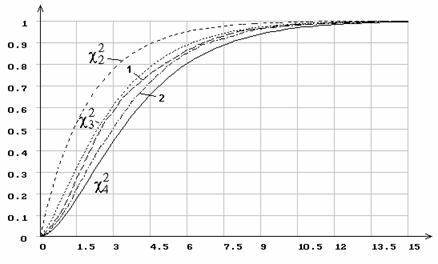
Рис. 4. Распределение статистики при 5 интервалах группирования

и оценивании масштабного параметра распределения наибольшего значения.

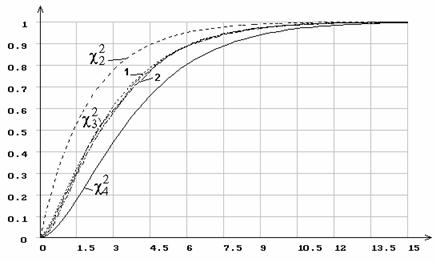
Рис. 5. Распределение статистики при 5 интервалах группирования

и оценивании параметра сдвига распределения наибольшего значения.

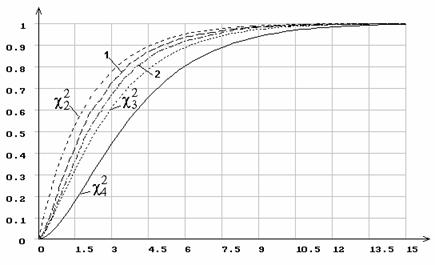
Рис. 6. Распределение статистики при 5 интервалах группирования

и оценивании двух параметров распределения наибольшего значения.

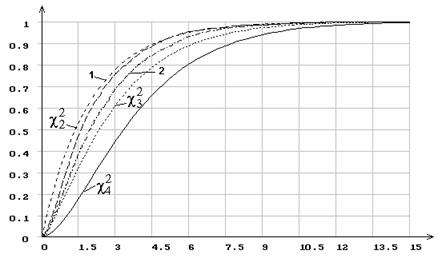
Рис. 7. Распределение статистики  при 5 интервалах группирования

и оценивании двух параметров нормального распределения.

            Какие изменения происходят с исследуемыми распределениями статистик с ростом числа интервалов? На рис. 8-10 приведены распределения статистики  при 7 интервалах группирования и оценивании параметров нормального распределения (моделировалась серия из  выборок объемом ). Распределения статистики  при 7 интервалах группирования в случае оценивания двух параметров нормального распределения представлены на рис. 11, на котором наблюдается аналогичная картина.

            Результаты моделирования и анализа указывают на то, что предельные распределения статистик обоих рассматриваемых критериев существенно отличаются при различных способах группирования (при вычислении оценок по негруппированным данным). При этом эмпирический закон распределения статистики при асимптотически оптимальном группировании ближе к теоретическому -распределению, чем при равновероятном группировании. Мало того, распределения статистик зависят не только от количества оцененных по выборке параметров, но и от того, какой параметр оценивался. Например, оценивание параметра сдвига приводит к более значительному изменению распределения статистики, чем оценивание масштабного параметра.

            Следует отметить, что эмпирические распределения статистики отношения правдоподобия оказываются ближе к предельному теоретическому -распределению, чем соответствующие эмпирические распределения статистики  Пирсона.

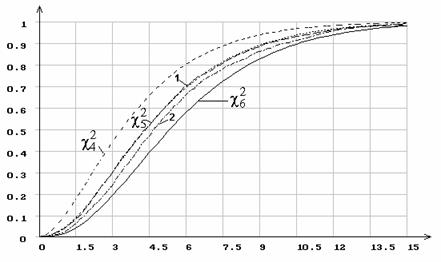
Рис. 8. Распределение статистики при 7 интервалах группирования

и оценивании масштабного параметра нормального распределения.

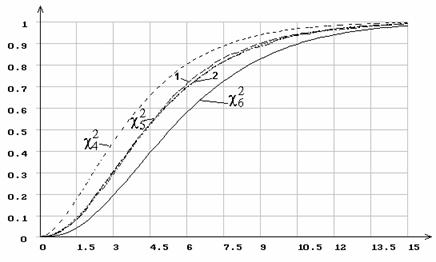
Рис. 9. Распределение статистики при 7 интервалах группирования

и оценивании параметра сдвига нормального распределения.

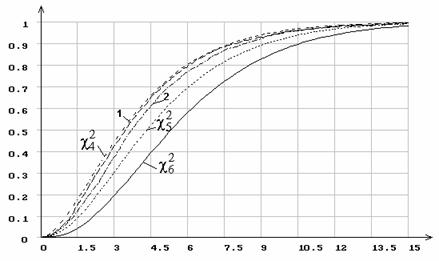
Рис. 10. Распределение статистики при 7 интервалах группирования

и оценивании двух параметров нормального распределения.

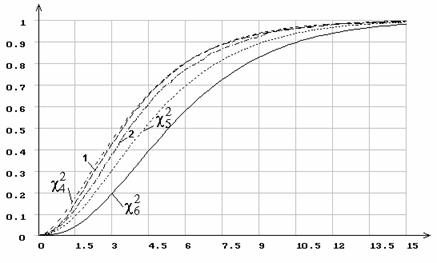
Рис. 11. Распределение статистики  при 7 интервалах группирования

и оценивании двух параметров нормального распределения.

-распределение с числом степеней свободы  является частным случаем гамма-распределения с основным параметром, равным , и масштабным - . Оценивание одного из параметров учитывается уменьшением числа степеней свободы на 1. На самом деле, если измерять изменение предельного закона “в степенях свободы”,  то оказывается, что оценивание даже параметра сдвига обычно приводит к изменению “числа степеней” на величину меньшую 1, еще к меньшему изменению в степенях свободы приводит оценивание масштабного параметра. Это особенно заметно при оценивании 2-х параметров и указывает на то, что использование в критериях согласия -распределения может сопровождаться занижением вероятности вида  и определенным риском отвергнуть верную гипотезу . Занижение более существенно при меньшем числе интервалов группирования. В целом этот риск существенно меньше в случае применения асимптотически оптимального группирования.

            При идентификации типов предельных законов распределения  статистик использовалось множество законов и семейств распределений, включенных в программную систему [8]. Эмпирические законы распределения статистик рассматриваемых критериев практически всегда с достаточно высокой точностью описываются гамма-распределением, то есть эмпирическая функция статистики очень хорошо согласуется с теоретическим законом по всем используемым в системе критериям согласия.

            В табл. 1-2 сведены результаты идентификации законов, соответственно, для статистик критериев  Пирсона и отношения правдоподобия при 5-ти интервалах группирования в случае асимптотически оптимального (АОГ) и равновероятного группирования (РВГ). В соответствующих клетках таблиц приведены значения параметров гамма-распределения с функцией плотности

.

Примечание 1. -распределение является частным случаем гамма-распределения, в котором  и число степеней свободы равно 2.

На первом месте указаны параметры гамма-распределения, в котором по эмпирическому распределению оценивался параметр , позволяющий судить о действительном “числе степеней свободы”, на втором - параметры гамма-распределения, согласие с которым наилучшее. По приводимым значениям параметров можно судить об отличии предельного распределения от соответствующего .

            В работе исследовались распределения статистик при принадлежности наблюдаемой выборки различным законам. В таблицах представлены распределения статистик, когда наблюдаемые случайные величины распределены в соответствии с законами: нормальным, с функцией плотности  - ; Коши - ; наибольшего значения - 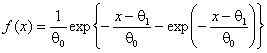 и логистическим - .

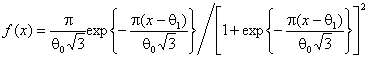Таблица 1

Предельные распределения статистики  Пирсона при
№ п/п	Распредел-е случайной величины	Параметры по выборке не оценивались	Оценивался только масштабный параметр	Оценивался только параметр сдвига	Оценивалось два параметра
1.	Нормальное (АОГ)	1.9443, 0.5, 0.0 1.9482, 0.5011, 0.0	1.6810, 0.5, 0.0 1.7471, 0.5267, 0.0	1.6493, 0.5, 0.0 1.7263, 0.5318, 0.0	1.2165, 0.5, 0.0 1.4498, 0.6465, 0.0
2.	Нормальное (РВГ)	2.0421, 0.5, 0.0 1.9940, 0.4851, 0.0	1.8134, 0.5, 0.0 1.9394, 0.5463, 0.0	1.6009, 0.5, 0.0 1.6336, 0.5142, 0.0	1.3635, 0.5, 0.0 1.5358, 0.5922, 0.0
3.	Логистич-кое (АОГ)	1.9898, 0.5, 0.0 1.9090, 0. 4737, 0.0	1.6028, 0.5, 0.0 1.6070, 0.5019, 0.0	1.5466, 0.5, 0.0 1.5847, 0.5173, 0.0	1.2215, 0.5, 0.0 1.4158, 0.6212, 0.0
4.	Логистич-кое (РВГ)	2.0352, 0.5, 0.0 1.9662, 0.4785, 0.0	1.7786,0.5, 0.0 1.8281, 0.5189, 0.0	1.5523, 0.5, 0.0 1.6144, 0.5278, 0.0	1.2904, 0.5, 0.0 1.4974, 0.6196, 0.0
5.	Коши (АОГ)	2.0534, 0.5, 0.0 1.9470, 0.4667, 0.0	1.5906, 0.5, 0.0 1.5730, 0.4925, 0.0	1.5177, 0.5, 0.0 1.6500, 0.5609, 0.0	1.1623, 0.5, 0.0 1.3585, 0.6312, 0.0
6.	Коши (РВГ)	2.0534, 0.5, 0.0 1.9465, 0.4667, 0.0	1.6204, 0.5, 0.0 1.6658, 0.5195, 0.0	1.5681, 0.5, 0.0 1.6482, 0.5353, 0.0	1.1470, 0.5, 0.0 1.2997, 0.6039, 0.0
7.	Наибольшего знач. (АОГ)	1.9942, 0.5, 0.0 2.0244, 0.5100, 0.0	1.6547, 0.5, 0.0 1.7134, 0.5245, 0.0	1.5573, 0.5, 0.0 1.5758, 0.5085, 0.0	1.2721, 0.5, 0.0 1.4362, 0.5965, 0.0
8.	Наибольшего знач. (РВГ)	2.0364, 0.5, 0.0 2.0144, 0.4932, 0.0	1.8152, 0.5, 0.0 1.8991, 0.5308, 0.0	1.5916, 0.5, 0.0 1.6751, 0.5361, 0.0	1.3674, 0.5, 0.0 1.4200, 0.5280, 0.0

Таблица 2

Предельные распределения статистики отношения правдоподобия при
№ п/п	Распредел-е случайной величины	Параметры по выборке не оценивались	Оценивался только масштабный параметр	Оценивался только параметр сдвига	Оценивалось два параметра
1.	Нормальное (АОГ)	1.9307, 0.5, 0.0 1.9463, 0.5054, 0.0	1.6568, 0.5, 0.0 1.7959, 0.5572, 0.0	1.6419, 0.5, 0.0 1.7388, 0.5403, 0.0	1.2150, 0.5, 0.0 1.4646, 0.6571, 0.0
2.	Нормальное (РВГ)	2.0357, 0.5, 0.0 1.9958, 0.4877, 0.0	1.8083, 0.5, 0.0 1.9491, 0.5518, 0.0	1.5986, 0.5, 0.0 1.6383, 0.5171, 0.0	1.3458, 0.5, 0.0 1.4769, 0.5713, 0.0
3.	Логистич-кое (АОГ)	1.9808, 0.5, 0.0 1.9159, 0.4789, 0.0	1.5913, 0.5, 0.0 1.6344, 0.5188, 0.0	1.5426, 0.5, 0.0 1.5931, 0.5229, 0.0	1.2176, 0.5, 0.0 1.4276, 0.6316, 0.0
4.	Логистич-кое (РВГ)	2.0300, 0.5, 0.0 1.9715, 0.4818, 0.0	1.7750, 0.5, 0.0 1.8385, 0.5241, 0.0	1.5233, 0.5, 0.0 1.5246, 0.5004, 0.0	1.2878, 0.5, 0.0 1.5059, 0.6266, 0.0
5.	Коши (АОГ)	2.0458, 0.5, 0.0 1.9625, 0.4740, 0.0	1.5889, 0.5, 0.0 1.5688, 0.4916, 0.0	1.5100, 0.5, 0.0 1.6625, 0.5707, 0.0	1.1598, 0.5, 0.0 1.3664, 0.6387, 0.0
6.	Коши (РВГ)	2.0458, 0.5, 0.0 1.9623, 0.4740, 0.0	1.6169, 0.5, 0.0 1.6779, 0.5259, 0.0	1.5649, 0.5, 0.0 1.6506, 0.5378, 0.0	1.1471, 0.5, 0.0 1.3166, 0.6154, 0.0
7.	Наибольшего знач. (АОГ)	1.9734, 0.5, 0.0 2.0228, 0.5165, 0.0	1.6201, 0.5, 0.0 1.7708, 0.5638, 0.0	1.5415, 0.5, 0.0 1.6039, 0.5283, 0.0	1.2642, 0.5, 0.0 1.4643, 0.6190, 0.0
8.	Наибольшего знач. (РВГ)	2.0303, 0.5, 0.0 2.0201, 0.4970, 0.0	1.8109, 0.5, 0.0 1.9077, 0.5357, 0.0	1.5871, 0.5, 0.0 1.6721, 0.5368, 0.0	1.3599, 0.5, 0.0 1.4148, 0.5293, 0.0

            Как говорилось выше, использование в критериях согласия -распределения для вычисления вероятности вида  связано с риском отвергнуть верную гипотезу . В случае применения асимптотически оптимального группирования этот риск существенно меньше. В качестве примера в табл. 3 приводятся значения вероятностей  для различных значений статистики , вычисленные по -распределению и в соответствии с “действительными” распределениями статистик при 7 интервалах группирования и оценивании 2-х параметров нормального распределения. Эти данные, вместе с другими результатами, позволяют сделать вывод, что в случае применения асимптотически оптимального группирования и использования -распределения ошибки при вычислении вероятности  практически незначимы. На рис. 12-13 представлены гамма-распределения, описывающие соответствующие распределения статистики  при 7 интервалах в случае асимптотически оптимального и равновероятного группирования. На рисунках отражены функции плотности, гистограммы и результаты проверки гипотез о согласии по различным критериям. Эмпирические распределения и функции гамма-распределений не приводятся, так как визуально различия между ними не наблюдается.

Таблица 3

Значения вероятностей вида
Знач.	Распределение	Распределение статистики		Распределение статистики
		При АОГ	При РВГ	При АОГ	При РВГ
3	0.5578	0.5876	0.6293	0.5914	0.6304
4	0.4060	0.4303	0.4700	0.4356	0.4716
5	0.2873	0.3049	0.3384	0.3108	0.3403
6	0.1991	0.2108	0.2370	0.2165	0.2389
7	0.1359	0.1430	0.1626	0.1481	0.1643
8	0.0916	0.0956	0.1096	0.0999	0.1111
9	0.0611	0.0632	0.0729	0.0666	0.0741
10	0.0404	0.0413	0.0480	0.0440	0.0489
11	0.0266	0.0268	0.0313	0.0288	0.0320
12	0.0173	0.0173	0.0202	0.0187	0.0207
13	0.0113	0.0110	0.0130	0.0120	0.0133

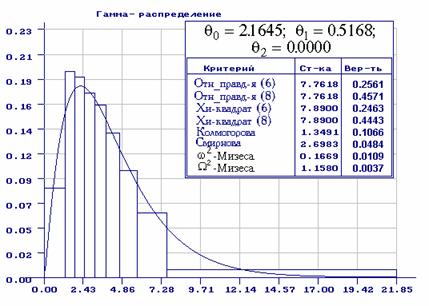
Рис. 12. Распределение статистики  при 7 интервалах асимптотически оптимального группирования в случае оценивания 2-х параметров нормального распределения

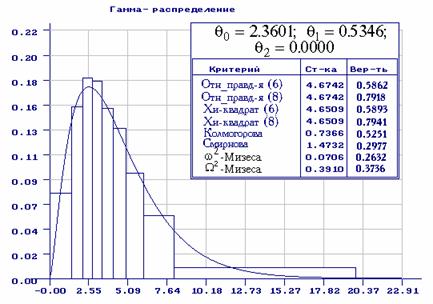
Рис. 13. Распределение статистики  при 7 интервалах равновероятного группирования в случае оценивания 2-х параметров нормального распределения

Примечание 2. При вычислении вероятностей вида , соответствующих непараметрическим критериям (см. рис. 12-13), использованы распределения соответствующих непараметрических статистик для значения параметра формы гамма-распределения  [11].

            Посмотрим, что будет происходить при дальнейшем увеличении числа интервалов. На рис. 14-16 приведены эмпирические распределения статистики  при 10 интервалах группирования и оценивании параметров нормального распределения (при справедливой гипотезе ). О степени близости эмпирических распределений статистики  соответствующим -распределениям можно судить по оценкам параметров гамма-распределения, полученным по смоделированным выборкам этой статистики и представленным в табл. 4 (в соответствии с нормальным распределением моделировалось  выборок объемом , число интервалов ). На первом месте указаны параметры гамма-распределения, в котором по эмпирическому распределению оценивался параметр , на втором -  параметры, где оценивались  и . Как видим, при 10 интервалах и оценивании одного параметра распределения статистики и при АОГ, и при РВГ достаточно близки к теоретическому   (разницы практически нет: см. рис.14-15 и табл.4). При оценивании одновременно 2-х параметров разница в распределениях еще заметна (причем для АОГ эмпирическое распределение даже выше теоретического ). Таким образом, при объеме выборки, позволяющем выбрать количество интервалов больше 10, при вычислении ОМП по негруппированным данным можно с уверенностью использовать в рассматриваемых критериях -распределение.

Таблица 4

Предельные распределения статистики  Пирсона при
Оцениваемый параметр нормального закона	Параметры “предельного” гамма-распределения при АОГ	Параметры “предельного” гамма-распределения при РВГ
Параметры не оценивались	4.5483, 0.5, 0.0 4.3343, 0.4732, 0.0	4.3599, 0.5, 0.0 4.3034, 0.4930, 0.0
Масштабный параметр	4.0724, 0.5, 0.0 3.9629, 0.4851, 0.0	4.0751, 0.5, 0.0 4.2553, 0.5253, 0.0
Параметр сдвига	4.0466, 0.5, 0.0 4.0395, 0.4995, 0.0	4.0332, 0.5, 0.0 4.0349, 0.5005, 0.0
Оба параметра	3.4717, 0.5, 0.0 3.4030, 0.4890, 0.0	3.6249, 0.5, 0.0 3.5647, 0.4909, 0.0

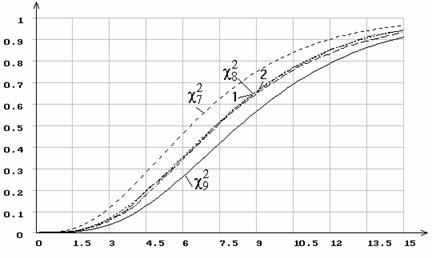
Рис. 14. Распределение статистики при 10 интервалах группирования

и оценивании масштабного параметра нормального распределения

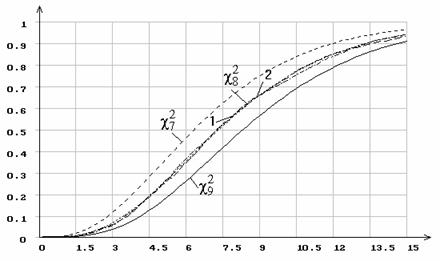
Рис. 15. Распределение статистики при 10 интервалах группирования

и оценивании параметра сдвига нормального распределения

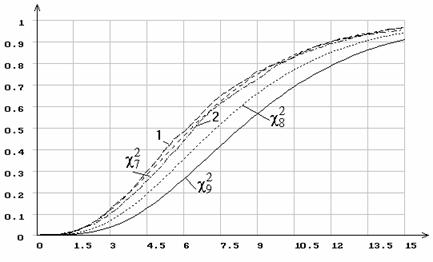
Рис. 16. Распределение статистики при 10 интервалах группирования

и оценивании двух параметров нормального распределения

            Посмотрим, как отражается способ группирования на предельных распределениях статистики  при справедливости альтернативной гипотезы . На рис. 17 приведены полученные в результате моделирования функции распределения  при использовании асимптотически оптимального и равновероятного группирования, когда гипотеза  состоит в том, что выборка принадлежит нормальному закону распределения (, ), а гипотеза  - логистическому (,).  Эти два закона достаточны близки и трудно различаются с помощью критериев согласия. На рис. 17 приведены эмпирические распределения статистики при простой гипотезе , а на рис. 18 - при сложной, когда оба параметра нормального закона оценивались по выборке. Количество интервалов группирования - 7. Из рисунков видно, насколько выше мощность критерия при асимптотически оптимальном группировании по сравнению равновероятным.

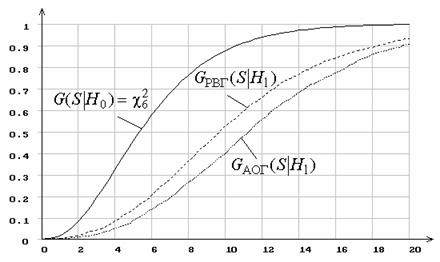
Рис. 17. Распределения статистики  при проверке простой гипотезы

            В работах [4,9,10] рекомендуется видоизменение стандартной статистики , при котором предельное распределение есть обычное распределение   с -й степенью свободы и в том случае, когда в качестве оценок используются оценки максимального правдоподобия параметров по негруппированным данным. При этом вектор  предполагается заданным и граничные точки интервалов определяются соотношениями , . Предложенная статистика имеет вид [9]

,

где матрица , и ее элементы и размерность определяются оцениваемыми компонентами вектора параметров ;  - элементы информационной матрицы Фишера; ;  - элементы вектора ;  - вычисляется в соответствии с (1).

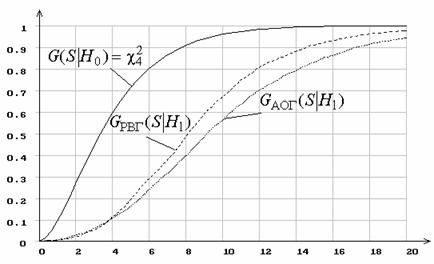
Рис. 18. Распределения статистики  при проверке сложной гипотезы

            Моделирование распределений статистики  при вычислении оценок максимального правдоподобия параметров по негруппированным данным показало, что её эмпирические распределения при верной нулевой гипотезе  также зависят от способа группирования. Но различие в распределениях статистик примерно того же порядка что при оценивании, что без оценивания параметров. В целом, результаты моделирования подтвердили, что законы распределения, описывающие выборки статистики , хорошо согласуются с -распределениям при обоих способах группирования. О степени близости можно судить по представленным в табл. 5 оценкам параметров гамма-распределения, полученным по смоделированным выборкам статистики  (: нормальное распределение, моделировалось  выборок объемом , число интервалов ).

Таблица 5

Оцениваемый параметр нормального закона	Параметры “предельного” гамма-распределения при АОГ	Параметры “предельного” гамма-распределения при РВГ
Параметры не оценивались	2.0508, 0.5302, 0.0	1.9855, 0.4770, 0.0
Масштабный параметр	2.0612, 0.4988, 0.0	1.9195, 0.4827, 0.0
Параметр сдвига	1.9702, 0.5063, 0.0	1.9833, 0.5035, 0.0
Оба параметра	1.9366, 0.5051, 0.0	2.0345, 0.5089, 0.0

            Распределения статистики  при справедливой конкурирующей гипотезе , также как и распределения статистики , существенно зависят от способа группирования.

Выводы

            Результаты моделирования и анализа показали, что если по наблюдаемой выборке не оценивались параметры закона, то распределения статистик критериев отношения правдоподобия и  Пирсона при справедливой гипотезе  достаточно хорошо согласуются с  как при равновероятном, так и при асимптотически оптимальном группировании. Различия между распределениями статистик при равновероятном и асимптотически оптимальном группировании заметны, но не значимы. При этом распределения статистик при равновероятном группировании в целом оказываются ближе к  распределению.

            В условиях, когда по негруппированным наблюдениям определяются оценки параметров, распределения этих статистик хорошо согласуются с гамма-распределениями. При этом:

1. Предельные распределения статистик критериев отношения правдоподобия и  Пирсона существенно зависят от способа группирования, особенно при малом числе интервалов.

2. Распределения статистик зависят не только от количества оцененных по выборке параметров, но и от того, какой параметр оценивался. Оценивание параметра сдвига приводит к более значительному изменению распределений статистик, чем оценивание масштабного параметра. Картина аналогичная той, что наблюдается для распределений статистик типа Колмогорова, Смтрнова и Мизеса [11].

3. Эмпирические распределения статистики отношения правдоподобия оказываются ближе к предельному теоретическому -распределению, чем соответствующие эмпирические распределения статистики  Пирсона.

4. В целом, при малом числе интервалов и оценивании  параметров число степеней свободы предельного распределения уменьшается на “число степеней свободы” меньшее . При этом эмпирический закон распределения статистики при асимптотически оптимальном группировании ближе к теоретическому -распределению, чем при равновероятном группировании. Это можно объяснить тем, что оценка, получаемая в результате минимизации статистики (1), в случае асимптотически оптимального группирования в общем должна быть ближе к оценке максимального правдоподобия по негруппированным данным, чем в случае равновероятного группирования.

5. С ростом числа интервалов  разность между функцией распределения  и действительными функциями распределения статистик отношения правдоподобия и  Пирсона в случае асимптотически оптимального группирования убывает существенно быстрее.

6. Численный анализ показал, что при использовании для вычисления вероятностей  функции распределения  при асимптотически оптимальном группировании и малом числе интервалов () при малых значениях (именно при малых вероятностях принимается решение отклонить гипотезу  или нет) погрешность имеет величины, которые не существенны для практических задач. То есть в этом случае, используя -распределение, мы не совершаем большой ошибки.

7. С ростом количества интервалов (при соответствующем объеме выборки) отличие предельных распределений от распределений  и при асимптотически оптимальном и при равновероятном группировании становится несущественным.

            Распределения статистик  и  при справедливой гипотезе  всегда (и с оцениванием параметров и без оценивания) сильно зависят от варианта группирования. Разность – при близких альтернативах и асимптотически оптимальном группировании максимальна, следовательно, максимальна мощность критерия [12].

Литература

1. Кендалл М., Стьюарт А. Статистические выводы и связи. - М.: Наука, 1973. - 900 с.

2. Chernoff H., Lehmann E.L. The use of maximum likelihood estimates in  test for goodness of fit // Ann. Math. Stat., 1954. V. 25. - P. 579-586.

3. Чибисов Д.М. Некоторые критерии типа хи-квадрат для непрерывных распределений // Теория вероятностей и ее применение. 1971. Т. XVI. № 1. - С. 3-20.

4. Никулин М.С. Критерий хи-квадрат для непрерывных распределений с параметрами сдвига и масштаба / Теория вероятностей и ее применение. 1973. Т. XVIII. № 3. С.583-591.

5. Денисов В.И., Лемешко Б.Ю., Цой Е.Б. Оптимальное группирование, оценка параметров и планирование регрессионных экспериментов: В 2 ч. / Новосиб. гос. техн. ун-т. - Новосибирск, 1993. - 346 с.

6. Mann H.B., Wald A. On the choice of the number of class intervals in the application of the chi square test // Ann. Math. Stat., 1942. V. 13. - P.306-317.

7. Б.Ю.Лемешко, С.Н.Постовалов. О влиянии способа группирования данных на распределения статистик  Пирсона и отношения правдоподобия // Мат. международной НТК “Информатика и проблемы телекоммуникаций”. - Новосибирск, 1997. - С. 120-123.

8. Лемешко Б.Ю. Статистический анализ одномерных наблюдений случайных величин: Программная система. - Новосибирск: Изд-во НГТУ. - 1995. - 125 с.

9. Никулин М.С. О критерии хи-квадрат для непрерывных распределений / Теория вероятностей и ее применение. 1973. Т. XVIII. № 3. С.675-676.

10.Мирвалиев М., Никулин М.С. Критерии согласия типа хи-квадрат / Заводская лаборатория. 1992. Т. 58. № 3. С.52-58.

11.Лемешко Б.Ю., Постовалов С.Н. О распределениях статистик непараметрических критериев согласия при оценивании по выборкам параметров наблюдаемых законов / Заводская лаборатория. (В печати)

12.Лемешко Б.Ю. Асимптотически оптимальное группирование наблюдений в критериях согласия //Заводская лаборатория, 1998. Т. 64. - №1. - С.56-64.

[Содержание]