См. также: Прикладная
математическая статистика (материалы к семинарам)
Заводская лаборатория. Диагностика материалов. 2001. Т. 67. - № 7. - С. 62-71.
УДК 519.24
О ЗАВИСИМОСТИ РАСПРЕДЕЛЕНИЙ СТАТИСТИК НЕПАРАМЕТРИЧЕСКИХ КРИТЕРИЕВ И ИХ МОЩНОСТИ ОТ МЕТОДА ОЦЕНИВАНИЯ ПАРАМЕТРОВ
Б.Ю. Лемешко, С.Н. Постовалов
Введение
Известно, что непараметрические критерии согласия (Колмогорова, Смирнова, ![]() и
и ![]() Мизеса) при оценивании по той же
выборке параметров распределений вероятностей, то есть при проверке сложных
гипотез, теряют свойство “свободы от распределения”. В такой ситуации
предельные распределения статистик этих критериев будут зависеть от закона,
которому подчинена наблюдаемая выборка. Точкой отсчета, с которой начались
исследования предельных (и допредельных) распределений статистик
непараметрических критериев согласия при сложных гипотезах, послужила работа
[1].
Мизеса) при оценивании по той же
выборке параметров распределений вероятностей, то есть при проверке сложных
гипотез, теряют свойство “свободы от распределения”. В такой ситуации
предельные распределения статистик этих критериев будут зависеть от закона,
которому подчинена наблюдаемая выборка. Точкой отсчета, с которой начались
исследования предельных (и допредельных) распределений статистик
непараметрических критериев согласия при сложных гипотезах, послужила работа
[1].
В литературе научного характера изложен ряд подходов к использованию непараметрических критериев согласия в этом случае.
При достаточно большой выборке ее можно разбить на две части и по одной из них оценивать параметры, а по другой проверять согласие. В случае больших объемов выборки такой подход оправдан [2]. Но если объем выборки относительно невелик, то способ разбиения ее на две части будет отражаться и на оценках параметров, и на распределениях статистик критериев согласия.
Для случая принадлежности выборки нормальному закону предельные распределения
статистики критерия типа ![]() Мизеса при
оценивании одного или обоих параметров по методу максимального правдоподобия
получены аналитически и табулированы [3].
Мизеса при
оценивании одного или обоих параметров по методу максимального правдоподобия
получены аналитически и табулированы [3].
В некоторых частных случаях проверки сложных гипотез, например, при оценивании параметров распределений экспоненциального, нормального, экстремальных значений, Вейбулла и некоторых других законов, таблицы процентных точек для предельных распределений статистик непараметрических критериев получены методом статистического моделирования [4-7].
В работах [8-11] для статистик типа Колмогорова для некоторых законов,
соответствующих гипотезе ![]() , получены
формулы для приближенного вычисления вероятностей “согласия” вида
, получены
формулы для приближенного вычисления вероятностей “согласия” вида ![]() , где
, где ![]() - вычисленное по выборке значение
соответствующей статистики
- вычисленное по выборке значение
соответствующей статистики ![]() . Эти формулы
дают достаточно хорошие приближения при малых значениях соответствующих
вероятностей. С помощью таких формул вычисляются вероятности вида
. Эти формулы
дают достаточно хорошие приближения при малых значениях соответствующих
вероятностей. С помощью таких формул вычисляются вероятности вида ![]() в пакете STADIA [12].
в пакете STADIA [12].
Нами в результате компьютерного моделирования распределений статистик
непараметрических критериев для ряда законов, соответствующих гипотезе ![]() , найдены аналитически простые модели,
которые хорошо аппроксимируют предельные распределения статистик
непараметрических критериев согласия в случае проверки сложных гипотез, когда
при оценивании по выборке параметров используется метод максимального
правдоподобия [13, 14].
, найдены аналитически простые модели,
которые хорошо аппроксимируют предельные распределения статистик
непараметрических критериев согласия в случае проверки сложных гипотез, когда
при оценивании по выборке параметров используется метод максимального
правдоподобия [13, 14].
Тем не менее, полученные более чем за 40 лет исследований таблицы процентных точек и предельные распределения статистик непараметрических критериев ограничены относительно узким кругом сложных гипотез. В самом деле, распределения статистик (или их процентные точки) при проверке сложных гипотез получены лишь для порядка 15 законов, в то время как множество вероятностных моделей, используемых в приложениях для описания реальных случайных величин, существенно шире.
Более того, для многих исследователей очевиден факт зависимости распределений статистик непараметрических критериев согласия от метода оценивания параметров. Следует также учитывать, что распределения статистик существенно зависят от объёма выборки. В настоящий момент вопросы применения непараметрических критериев согласия при проверке сложных гипотез в связи с различием в методах оценивания вообще не отражены в научных публикациях.
Исходя из вышесказанного, понятно, почему в отечественных и международных стандартах, регламентирующих применение статистических методов, нет указаний по использованию непараметрических критериев в случае проверки сложных гипотез. Тем более, нет указаний по учету нюансов, связанных с используемым методом оценивания.
Игнорирование на практике того, что проверяется сложная гипотеза, не учет фактов различия в сложных гипотезах, приводит к некорректному применению непараметрических критериев согласия и неверным статистическим выводам в приложениях. Предостережения против неаккуратного применения критериев согласия при проверке сложных гипотез неоднократно звучали на страницах “Заводской лаборатории” [15-17].
В работе [18], используя методы статистического моделирования, мы исследовали, как отражается объем наблюдаемой выборки на распределениях статистик непараметрических критериев согласия при простых и сложных гипотезах и как влияет на эти распределения применяемый метод оценивания параметров.
В данном случае мы попытаемся дать более полную картину того, что и как влияет на распределения статистик непараметрических критериев согласия. Полученное представление, надеемся, будет способствовать корректному применению непараметрических критериев согласия при любых сложных гипотезах и любых методах оценивания.
С использованием критериев согласия могут проверяться
простые гипотезы вида ![]() :
: ![]() , где
, где ![]() –
функция распределения вероятностей, с которой проверяется согласие наблюдаемой
выборки, а
–
функция распределения вероятностей, с которой проверяется согласие наблюдаемой
выборки, а ![]() – известное значение параметра (скалярного или
векторного), и сложные гипотезы
– известное значение параметра (скалярного или
векторного), и сложные гипотезы ![]() :
: ![]() , где
, где ![]() –
пространство параметров и оценка параметра
–
пространство параметров и оценка параметра ![]() вычисляется
по этой же самой выборке. Если оценка
вычисляется
по этой же самой выборке. Если оценка ![]() вычисляется
по другой выборке, то гипотеза простая. В процессе проверки по выборке
вычисляется значение
вычисляется
по другой выборке, то гипотеза простая. В процессе проверки по выборке
вычисляется значение ![]() статистики
используемого критерия. Далее, для того, чтобы сделать вывод о том, принять
или отклонить гипотезу
статистики
используемого критерия. Далее, для того, чтобы сделать вывод о том, принять
или отклонить гипотезу ![]() ,
необходимо знать условное распределение
,
необходимо знать условное распределение ![]() статистики
статистики
![]() при справедливости
при справедливости ![]() . И если вероятность
. И если вероятность
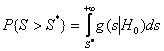
достаточно
большая, по крайней мере ![]() ,
где
,
где ![]() – условная плотность, а
– условная плотность, а ![]() – задаваемый уровень значимости (вероятность
ошибки первого рода – отклонить справедливую гипотезу
– задаваемый уровень значимости (вероятность
ошибки первого рода – отклонить справедливую гипотезу ![]() ), то принято считать, что нет оснований отклонять
гипотезу
), то принято считать, что нет оснований отклонять
гипотезу ![]() .
.
Если в процессе анализа выборки рассматривается некоторая
альтернатива ![]() :
: ![]() ,
то с ней связывают условное распределение
,
то с ней связывают условное распределение ![]() и
вероятность ошибки второго рода
и
вероятность ошибки второго рода ![]() (принять
гипотезу
(принять
гипотезу ![]() , в то время как верна гипотеза
, в то время как верна гипотеза ![]() ). Задание
). Задание ![]() для
применяемого критерия согласия однозначно определяет и
для
применяемого критерия согласия однозначно определяет и ![]() :
:
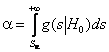 ,
, 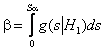 .
.
При
этом, чем больше мощность критерия ![]() ,
тем лучше он различает соответствующие гипотезы.
,
тем лучше он различает соответствующие гипотезы.
Как уже говорилось, распределения статистик
непараметрических критериев согласия при проверке сложных гипотез зависят от
характера этой сложной гипотезы. На закон распределения статистики ![]() влияет целый ряд факторов, определяющих
“сложность” гипотезы: вид наблюдаемого закона распределения
влияет целый ряд факторов, определяющих
“сложность” гипотезы: вид наблюдаемого закона распределения ![]() , соответствующего истинной гипотезе
, соответствующего истинной гипотезе ![]() ; тип оцениваемого параметра и количество оцениваемых
параметров; в некоторых ситуациях конкретное значение параметра, как, например,
в случае гамма-распределения; используемый метод оценивания параметров. При
малых объемах выборки
; тип оцениваемого параметра и количество оцениваемых
параметров; в некоторых ситуациях конкретное значение параметра, как, например,
в случае гамма-распределения; используемый метод оценивания параметров. При
малых объемах выборки ![]() распределение
распределение
![]() зависит и от
зависит и от ![]() .
Правда, существенная зависимость от
.
Правда, существенная зависимость от ![]() наблюдается
только при небольших объемах выборки. Уже при
наблюдается
только при небольших объемах выборки. Уже при ![]() распределение
распределение ![]() достаточно близко к предельному
достаточно близко к предельному ![]() , и зависимостью от
, и зависимостью от ![]() можно пренебречь.
можно пренебречь.
В случае задания конкретной альтернативы (конкурирующей гипотезы ![]() , которой соответствует распределение
, которой соответствует распределение ![]() ), функция распределения статистики
), функция распределения статистики ![]() также зависит от всех перечисленных факторов.
Но в отличие от
также зависит от всех перечисленных факторов.
Но в отличие от ![]() распределение статистики
распределение статистики ![]() при справедливой гипотезе
при справедливой гипотезе ![]() очень сильно зависит от объема выборки
очень сильно зависит от объема выборки ![]() . Именно благодаря этому с ростом
. Именно благодаря этому с ростом ![]() возрастает способность критериев различать
гипотезы, возрастает мощность критериев.
возрастает способность критериев различать
гипотезы, возрастает мощность критериев.
Как и в [14], в данной работе исследовались распределения статистик критериев типа
Колмогорова, Смирнова, ![]() и
и
![]() Мизеса. При изложении материала и использовании
терминов, относящихся к рассматриваемым критериям, мы старались следовать
рекомендациям работы [19]. При исследовании и моделировании эмпирических
распределений статистик
Мизеса. При изложении материала и использовании
терминов, относящихся к рассматриваемым критериям, мы старались следовать
рекомендациям работы [19]. При исследовании и моделировании эмпирических
распределений статистик ![]() ,
, ![]() , во всех приводимых ниже примерах, иллюстрирующих
распределения статистик критериев, количество моделируемых выборок
, во всех приводимых ниже примерах, иллюстрирующих
распределения статистик критериев, количество моделируемых выборок ![]() объема
объема ![]() выбиралось
равным 2000. Мы выбрали графическую форму иллюстрации материала, так как она
наиболее наглядно отображает изменения в законах распределения статистик в зависимости
от различных факторов. Цель данной работы еще раз заострить внимание
специалистов, использующих статистические методы в приложениях, на особенностях
применения непараметрических критериев при проверке сложных гипотез. В
дальнейшем мы планируем представить результаты аппроксимации законов
распределений исследуемых статистик для различных сложных гипотез, уточняющие
результаты, приведенные в [14], и расширяющие их в соответствии с излагаемыми в
данной статье новыми фактами.
выбиралось
равным 2000. Мы выбрали графическую форму иллюстрации материала, так как она
наиболее наглядно отображает изменения в законах распределения статистик в зависимости
от различных факторов. Цель данной работы еще раз заострить внимание
специалистов, использующих статистические методы в приложениях, на особенностях
применения непараметрических критериев при проверке сложных гипотез. В
дальнейшем мы планируем представить результаты аппроксимации законов
распределений исследуемых статистик для различных сложных гипотез, уточняющие
результаты, приведенные в [14], и расширяющие их в соответствии с излагаемыми в
данной статье новыми фактами.
Распределения статистик непараметрических критериев согласия при простых гипотезах
Распределение статистики
![]() ,
,
где
![]() – эмпирическая функция распределения,
– эмпирическая функция распределения, ![]() – теоретическая функция распределения,
– теоретическая функция распределения, ![]() – объём выборки, было получено Колмогоровым в
[20]. При
– объём выборки, было получено Колмогоровым в
[20]. При ![]() распределение статистики
распределение статистики ![]() сходится равномерно к распределению
Колмогорова с функцией распределения
сходится равномерно к распределению
Колмогорова с функцией распределения ![]() [21].
Наиболее часто в критерии Колмогорова (Колмогорова-Смирнова) используется
статистика вида [21]
[21].
Наиболее часто в критерии Колмогорова (Колмогорова-Смирнова) используется
статистика вида [21]
![]() ,
,
где
![]()
![]() -
объем выборки,
-
объем выборки, ![]() - упорядоченные по возрастанию выборочные
значения,
- упорядоченные по возрастанию выборочные
значения, ![]() - функция закона распределения, согласие с
которым проверяется. Распределение величины
- функция закона распределения, согласие с
которым проверяется. Распределение величины ![]() при простой гипотезе в пределе подчиняется
закону Колмогорова.
при простой гипотезе в пределе подчиняется
закону Колмогорова.
Статистика критерия Смирнова [21]
![]()
при
простой гипотезе в пределе подчиняется распределению ![]() с числом степеней свободы, равным 2.
с числом степеней свободы, равным 2.
Статистика критерия ![]() Мизеса
(Крамера-Мизеса-Смирнова)
Мизеса
(Крамера-Мизеса-Смирнова)
![]()
при простой гипотезе
подчиняется распределению ![]() [21],
а статистика критерия
[21],
а статистика критерия ![]() Мизеса
(Андерсона-Дарлинга)
Мизеса
(Андерсона-Дарлинга)
![]()
–
распределению ![]() [21].
[21].
Влияние объёма выборки на распределения статистик непараметрических критериев при простых и сложных гипотезах
Методами статистического моделирования нами была исследована зависимость распределений статистик непараметрических критериев от объема выборки при проверке различных простых и сложных гипотез.
Например, на рис. 1 показано, как при увеличении объёма выборки (![]() =5,10,20) меняется распределение
=5,10,20) меняется распределение ![]() статистики Колмогорова
статистики Колмогорова ![]() в случае проверки простой гипотезы
о принадлежности выборки нормальному закону. На рисунке отражена также
предельное распределение статистики – функция распределения Колмогорова
в случае проверки простой гипотезы
о принадлежности выборки нормальному закону. На рисунке отражена также
предельное распределение статистики – функция распределения Колмогорова ![]() . Эмпирические распределения
. Эмпирические распределения ![]() при больших
при больших ![]() практически сливаются с
практически сливаются с ![]() и на рисунке не показаны. Как
видим, при малых
и на рисунке не показаны. Как
видим, при малых ![]() распределение существенно отличается
от предельного, но уже при
распределение существенно отличается
от предельного, но уже при ![]() ошибка при
вычислении вероятности “согласия”
ошибка при
вычислении вероятности “согласия” ![]() оказывается
достаточно малой. Та же самая картина наблюдается в случае проверки сложных
гипотез о согласии. На рис. 2 при
оказывается
достаточно малой. Та же самая картина наблюдается в случае проверки сложных
гипотез о согласии. На рис. 2 при ![]() = 5, 10, 20,
1000 представлены распределения
= 5, 10, 20,
1000 представлены распределения ![]() статистики
типа Колмогорова
статистики
типа Колмогорова ![]() в случае проверки аналогичной, но
уже сложной, гипотезы о нормальности, когда по выборке вычисляются оценки
максимального правдоподобия (ОМП) параметров нормального закона.
в случае проверки аналогичной, но
уже сложной, гипотезы о нормальности, когда по выборке вычисляются оценки
максимального правдоподобия (ОМП) параметров нормального закона.
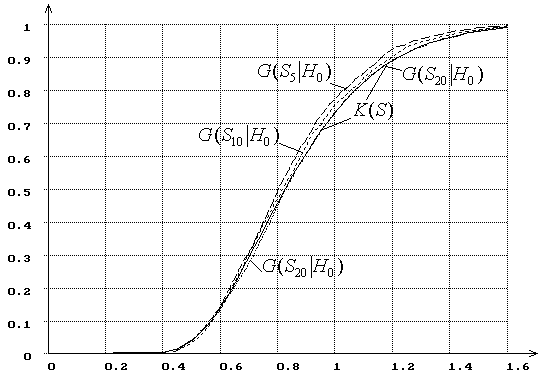
Рис. 1. Зависимость от ![]() распределений
распределений ![]() статистики
статистики ![]() Колмогорова
при простой гипотезе (
Колмогорова
при простой гипотезе (![]() -
нормальное распределение):
-
нормальное распределение): ![]() =
5, 10, 20,
=
5, 10, 20, ![]() .
.
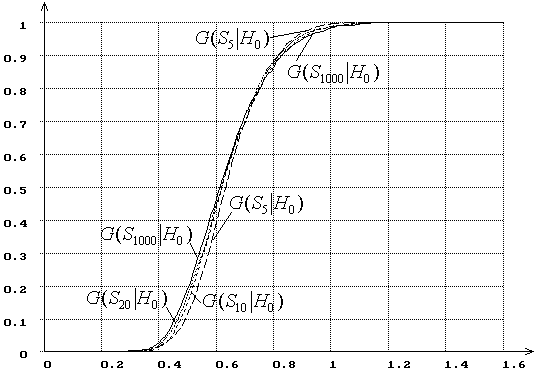
Рис. 2. Зависимость от ![]() распределений
распределений ![]() статистики критерия типа Колмогорова
статистики критерия типа Колмогорова ![]() при сложной гипотезе (
при сложной гипотезе (![]() - нормальное распределение, ОМП):
- нормальное распределение, ОМП): ![]() = 5, 10, 20, 1000.
= 5, 10, 20, 1000.
Следует отметить, что при малых ![]() наибольшие
отклонения от предельных распределений наблюдаются на “хвостах”. И при
простых, и при сложных гипотезах с ростом
наибольшие
отклонения от предельных распределений наблюдаются на “хвостах”. И при
простых, и при сложных гипотезах с ростом ![]() распределения
распределения
![]() равномерно сходятся к предельному.
Но если в случае простых гипотез с ростом
равномерно сходятся к предельному.
Но если в случае простых гипотез с ростом ![]() увеличивается
вероятность больших значений статистик, то в случае сложных возрастают вероятности
и больших, и малых значений статистик. Последнее замечание справедливо для
распределений статистик
увеличивается
вероятность больших значений статистик, то в случае сложных возрастают вероятности
и больших, и малых значений статистик. Последнее замечание справедливо для
распределений статистик ![]() ,
, ![]() ,
, ![]() .
.
Рис. 3
иллюстрирует изменения с ростом ![]() распределений
распределений
![]() статистики типа
статистики типа ![]() Мизеса
Мизеса ![]() при проверке сложной гипотезы о
нормальности и использовании при оценивании параметров метода максимального
правдоподобия. Чтобы подчеркнуть разницу в распределениях статистик при простых
и сложных гипотезах, на рисунке приведены
при проверке сложной гипотезы о
нормальности и использовании при оценивании параметров метода максимального
правдоподобия. Чтобы подчеркнуть разницу в распределениях статистик при простых
и сложных гипотезах, на рисунке приведены ![]() при
при ![]() = 5, 20, 1000 и
= 5, 20, 1000 и ![]() – предельная функция распределения
статистики
– предельная функция распределения
статистики ![]() при проверке простой гипотезы.
при проверке простой гипотезы.
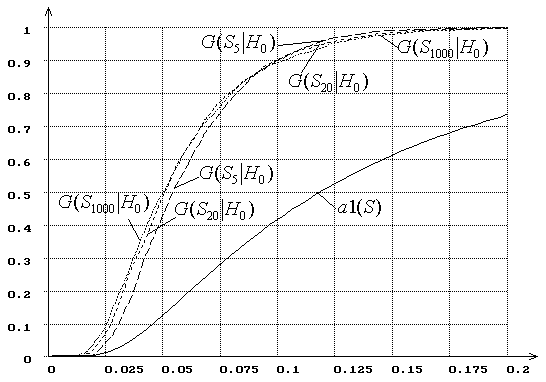
Рис. 3. Зависимость от ![]() распределений
распределений ![]() статистики типа
статистики типа ![]() Мизеса
Мизеса ![]() при
сложной гипотезе (
при
сложной гипотезе (![]() - нормальное распределение, ОМП):
- нормальное распределение, ОМП): ![]() = 5, 20, 1000.
= 5, 20, 1000.
Таким образом, проведенные исследования позволяют утверждать, что распределения
![]() статистик непараметрических
критериев (и типа Колмогорова, и типа
статистик непараметрических
критериев (и типа Колмогорова, и типа ![]() Мизеса)
при простых и сложных гипотезах очень быстро сходятся к предельным законам, и
уже при
Мизеса)
при простых и сложных гипотезах очень быстро сходятся к предельным законам, и
уже при ![]() можно, не опасаясь больших ошибок,
пользоваться этими предельными законами при анализе данных.
можно, не опасаясь больших ошибок,
пользоваться этими предельными законами при анализе данных.
Однако последний вывод не означает, что при малых объемах выборок с помощью этих критериев можно успешно различать близкие гипотезы. О трудности различения близких законов распределения, в частности, с помощью критерия согласия Колмогорова подчеркивалось в работе [22].
Влияние объема выборки на мощность непараметрических критериев при простых и сложных гипотезах
Способность
различать близкие гипотезы зависит от того, насколько сильно отличаются
распределения ![]() и
и ![]() .
.
Рассмотрим две
близкие гипотезы: ![]() - нормальное распределение с
плотностью
- нормальное распределение с
плотностью 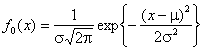 и параметрами
и параметрами ![]() ,
, ![]() ;
; ![]() - логистическое с такими же
параметрами
- логистическое с такими же
параметрами ![]() ,
, ![]() и
плотностью
и
плотностью 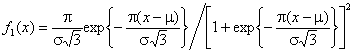 . О близости этих законов
распределения можно судить по рис. 4, на котором представлены их функции
распределения. Рис. 5. иллюстрирует зависимость от
. О близости этих законов
распределения можно судить по рис. 4, на котором представлены их функции
распределения. Рис. 5. иллюстрирует зависимость от ![]() распределений
распределений ![]() статистики
статистики ![]() Колмогорова при проверке простой
гипотезы
Колмогорова при проверке простой
гипотезы ![]() (
(![]() = 20, 100, 500, 1000), а рис. 6 – при
проверке сложной (при использовании ОМП).
= 20, 100, 500, 1000), а рис. 6 – при
проверке сложной (при использовании ОМП).
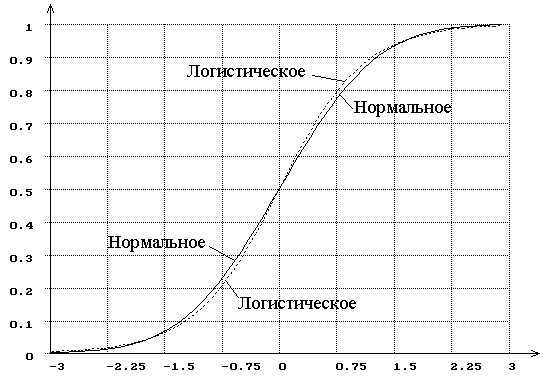
Рис. 4. Функции распределения нормального и логистического законов
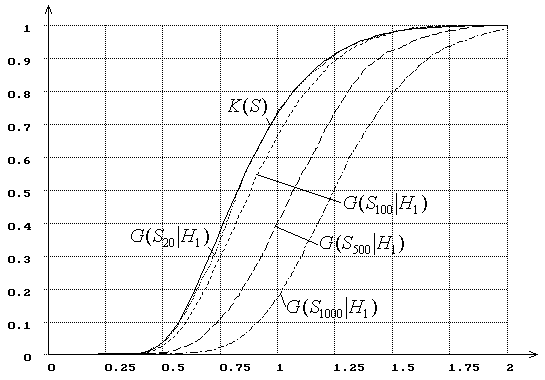
Рис. 5. Зависимость от ![]() распределений
распределений ![]() статистики
статистики ![]() Колмогорова
при простой гипотезе (
Колмогорова
при простой гипотезе (![]() -
нормальное распределение,
-
нормальное распределение, ![]() -
логистическое):
-
логистическое): ![]() = 20, 100, 500, 1000.
= 20, 100, 500, 1000.
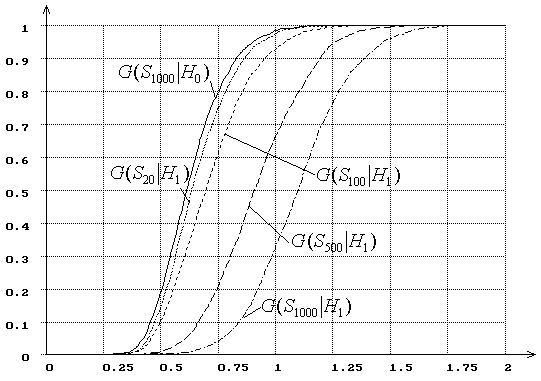
Рис. 6. Зависимость от ![]() распределений
распределений ![]() статистики критерия типа Колмогорова
статистики критерия типа Колмогорова ![]() при сложной гипотезе (
при сложной гипотезе (![]() - нормальное распределение,
- нормальное распределение, ![]() - логистическое, ОМП):
- логистическое, ОМП):
![]() = 20, 100, 500, 1000.
= 20, 100, 500, 1000.
Подчеркнем два
очевидных момента, которые подтверждаются результатами исследований и отражены
на рис. 5-6. Во-первых, ясно, что при малых выборках пытаться различать с
помощью непараметрических критериев согласия близкие гипотезы (особенно
простые) абсолютно бесполезно. Во-вторых, мощность непараметрических критериев
при проверке сложных гипотез при тех же объемах выборок ![]() всегда на порядок выше, чем при
проверке простых.
всегда на порядок выше, чем при
проверке простых.
Для сравнения на
рис. 7-8 представлены распределения ![]() статистики
статистики
![]() при проверке простой (рис. 7) и
сложной гипотезы (рис. 8) для тех же самых альтернатив
при проверке простой (рис. 7) и
сложной гипотезы (рис. 8) для тех же самых альтернатив ![]() и
и ![]() . Интересно отметить, что для данной
пары альтернатив в случае проверки сложной гипотезы критерий согласия типа
. Интересно отметить, что для данной
пары альтернатив в случае проверки сложной гипотезы критерий согласия типа ![]() Мизеса обладает несколько большей
мощностью при различении близких гипотез, чем критерий типа Колмогорова, а
в случае простых – наоборот.
Мизеса обладает несколько большей
мощностью при различении близких гипотез, чем критерий типа Колмогорова, а
в случае простых – наоборот.
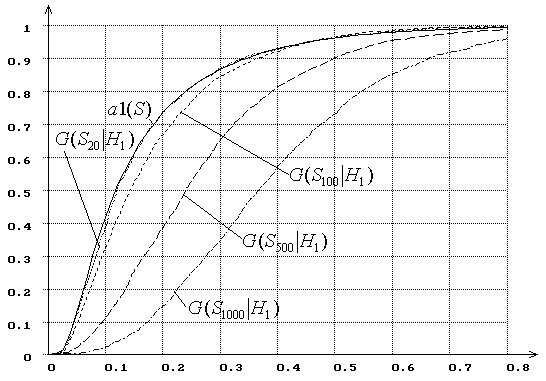
Рис. 7. Зависимость от ![]() распределений
распределений ![]() статистики
статистики ![]() Мизеса
Мизеса
![]() при простой гипотезе (
при простой гипотезе (![]() - нормальное распределение,
- нормальное распределение, ![]() - логистическое):
- логистическое):
![]() = 20, 100, 500, 1000.
= 20, 100, 500, 1000.
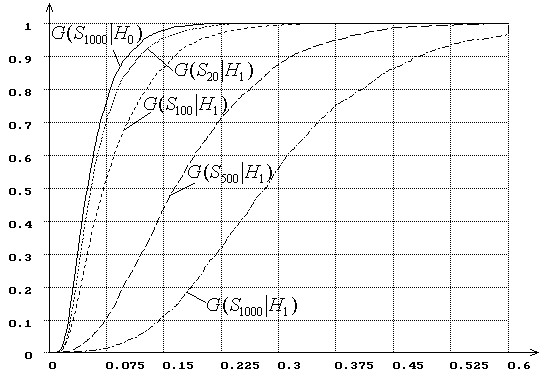
Рис. 8. Зависимость от ![]() распределений
распределений ![]() статистики типа
статистики типа ![]() Мизеса
Мизеса ![]() при
сложной гипотезе (
при
сложной гипотезе (![]() - нормальное распределение,
- нормальное распределение, ![]() - логистическое, ОМП):
- логистическое, ОМП): ![]() = 20, 100, 500, 1000.
= 20, 100, 500, 1000.
Отметим попутно,
что при проверке простых гипотез непараметрические критерии типа
Колмогорова, Смирнова, ![]() и
и ![]() Мизеса уступают по мощности
критериям типа
Мизеса уступают по мощности
критериям типа ![]() , особенно, если в последних используется
асимптотически оптимальное группирование [23-25], но при проверке сложных –
непараметрические критерии оказываются более мощными. Для того, чтобы
воспользоваться их преимуществами, надо только знать распределение
, особенно, если в последних используется
асимптотически оптимальное группирование [23-25], но при проверке сложных –
непараметрические критерии оказываются более мощными. Для того, чтобы
воспользоваться их преимуществами, надо только знать распределение ![]() при проверяемой сложной гипотезе.
при проверяемой сложной гипотезе.
Влияние метода оценивания на распределения статистик непараметрических критериев при сложных гипотезах
Распределения
статистик критериев согласия существенно зависят от метода оценивания
параметров. Строго говоря, каждому типу оценок при конкретной сложной
проверяемой гипотезе соответствует своё предельное распределение ![]() статистики. Нами исследовалось
влияние на распределения статистик различных методов оценивания. В данном
случае по следующим причинам при проверке сложных гипотез сравниваются
результаты использования ОМП и MD-оценок. Оценки
максимального правдоподобия наиболее предпочтительны благодаря своим
асимптотическим свойствам [26,27]. В случае MD-оценок
может минимизироваться значение статистики, используемой в критерии, то есть
будет получено распределение минимума соответствующей статистики.
статистики. Нами исследовалось
влияние на распределения статистик различных методов оценивания. В данном
случае по следующим причинам при проверке сложных гипотез сравниваются
результаты использования ОМП и MD-оценок. Оценки
максимального правдоподобия наиболее предпочтительны благодаря своим
асимптотическим свойствам [26,27]. В случае MD-оценок
может минимизироваться значение статистики, используемой в критерии, то есть
будет получено распределение минимума соответствующей статистики.
ОМП вычисляются
в результате максимизации по ![]() функции
правдоподобия
функции
правдоподобия
![]()
или её логарифма
![]() .
.
Чаще всего ОМП определяются в случае скалярного параметра как решение уравнения, а в случае векторного параметра как решение системы уравнений правдоподобия вида
![]() ,
(1)
,
(1)
где ![]() –
размерность вектора параметров
–
размерность вектора параметров ![]() . В общем случае
эта система оказывается нелинейной и, за редким исключением, решается только
численно.
. В общем случае
эта система оказывается нелинейной и, за редким исключением, решается только
численно.
Сделаем важное замечание, которое следует иметь ввиду. В данном случае, как и в [14], при проведении исследований ОМП вычислялись как решение системы (1). Использование же различных приближений ОМП соответственно отразится на распределениях статистик и свойствах критериев. В частности, вопросом отдельного исследования является проверка того, насколько сильно будут меняться распределения статик критериев согласия в случае применения одношаговых оценок [28], являющихся приближениями ОМП.
При вычислении MD-оценок минимизируется соответствующее расстояние
между эмпирическим и теоретическим распределениями. При использовании
статистики Колмогорова ![]() в качестве
оценки вектора параметров
в качестве
оценки вектора параметров ![]() выбираются
значения, минимизирующие эту статистику:
выбираются
значения, минимизирующие эту статистику:
![]()
(MD-оценки
![]() ). Аналогично, при использовании
статистики
). Аналогично, при использовании
статистики ![]() минимизируется по
минимизируется по ![]() статистика
статистика ![]() :
:
![]()
(MD-оценки
![]() ).
).
Влияние метода
оценивания на распределение статистики иллюстрирует рис. 9, на котором показаны
полученные в результате моделирования плотности распределения ![]() статистики критерия типа
Колмогорова
статистики критерия типа
Колмогорова ![]() при вычислении оценок параметра сдвига
нормального распределения тремя различными методами: минимума статистики
при вычислении оценок параметра сдвига
нормального распределения тремя различными методами: минимума статистики ![]() (график отмечен цифрой “1”),
минимума статистики
(график отмечен цифрой “1”),
минимума статистики ![]() (“2”) и максимального
правдоподобия (“3”). На рисунке через
(“2”) и максимального
правдоподобия (“3”). На рисунке через ![]() обозначена функция плотности
распределения Колмогорова.
обозначена функция плотности
распределения Колмогорова.
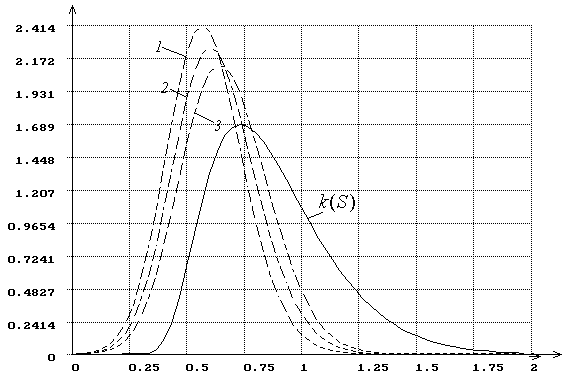
Рис. 9.
Плотности распределения ![]() статистики
критерия типа Колмогорова
статистики
критерия типа Колмогорова ![]() при
проверке сложной гипотезы (
при
проверке сложной гипотезы (![]() - нормальное
распределение, оценивается параметр сдвига: 1 - с использованием MD-оценок
- нормальное
распределение, оценивается параметр сдвига: 1 - с использованием MD-оценок ![]() , 2 - с
использованием MD-оценок
, 2 - с
использованием MD-оценок ![]() , 3 - с использованием ОМП)
, 3 - с использованием ОМП)
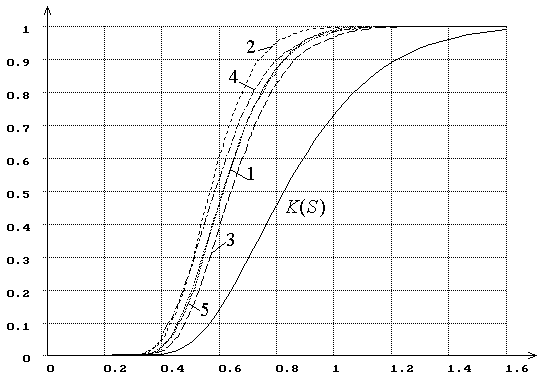
Рис. 10. Распределения ![]() статистики критерия типа Колмогорова
статистики критерия типа Колмогорова ![]() при оценивании двух параметров закона,
соответствующего гипотезе
при оценивании двух параметров закона,
соответствующего гипотезе ![]() (1
– нормального, 2 – логистического, 3 – Лапласа, 4 – наименьшего значения, 5 –
Коши). При использовании ОМП.
(1
– нормального, 2 – логистического, 3 – Лапласа, 4 – наименьшего значения, 5 –
Коши). При использовании ОМП.
На рис. 10 представлены распределения ![]() статистики
типа Колмогорова
статистики
типа Колмогорова ![]() при проверке сложной гипотезы с использованием
метода максимального правдоподобия для оценивания двух параметров закона,
соответствующего гипотезе
при проверке сложной гипотезы с использованием
метода максимального правдоподобия для оценивания двух параметров закона,
соответствующего гипотезе ![]() (1
– нормального, 2 – логистического, 3 – Лапласа с плотностью
(1
– нормального, 2 – логистического, 3 – Лапласа с плотностью ![]() , 4 – наименьшего значения с плотностью
, 4 – наименьшего значения с плотностью 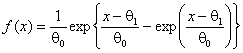 , 5 – Коши с функцией плотности
, 5 – Коши с функцией плотности ![]() . На рис. 11 представлены распределения
. На рис. 11 представлены распределения ![]() той же статистики
той же статистики ![]() при проверке тех же гипотез, но с использованием
MD-оценок параметров, полученных минимизацией по
параметрам статистики
при проверке тех же гипотез, но с использованием
MD-оценок параметров, полученных минимизацией по
параметрам статистики ![]() .
.
На рис. 12 приведены распределения статистики типа ![]() Мизеса
Мизеса ![]() для
аналогичных гипотез
для
аналогичных гипотез ![]() при
использовании ОМП, а на рис. 13 – при использовании MD-оценок, минимизирующих по параметрам статистику
при
использовании ОМП, а на рис. 13 – при использовании MD-оценок, минимизирующих по параметрам статистику ![]() .
.
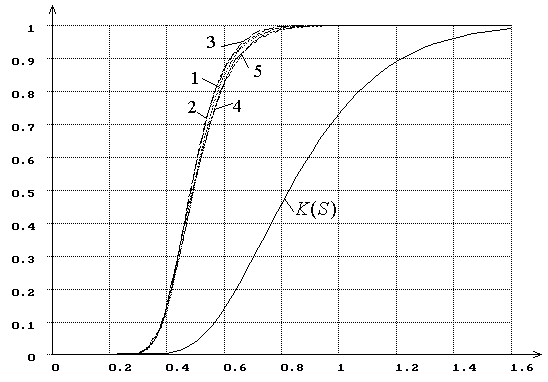
Рис. 11. Распределения ![]() статистики критерия типа Колмогорова
статистики критерия типа Колмогорова ![]() при оценивании двух параметров закона,
соответствующего гипотезе
при оценивании двух параметров закона,
соответствующего гипотезе ![]() (1
– нормального, 2 – логистического, 3 – Лапласа, 4 – наименьшего значения, 5 –
Коши). При использовании MD-оценок
(1
– нормального, 2 – логистического, 3 – Лапласа, 4 – наименьшего значения, 5 –
Коши). При использовании MD-оценок ![]() .
.
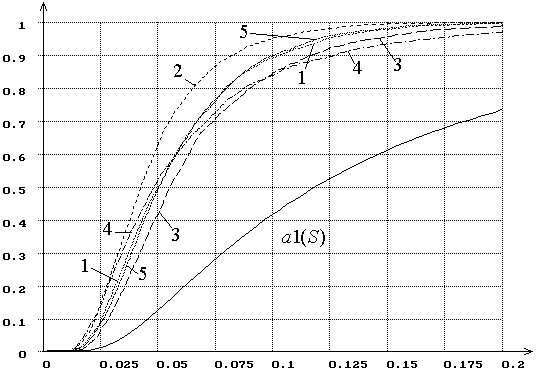
Рис. 12. Распределения ![]() статистики критерия типа
статистики критерия типа ![]() Мизеса
Мизеса ![]() при
оценивании двух параметров закона, соответствующего гипотезе
при
оценивании двух параметров закона, соответствующего гипотезе ![]() (1 – нормального, 2 – логистического, 3 –
Лапласа, 4 – наименьшего значения, 5 – Коши). При использовании ОМП.
(1 – нормального, 2 – логистического, 3 –
Лапласа, 4 – наименьшего значения, 5 – Коши). При использовании ОМП.
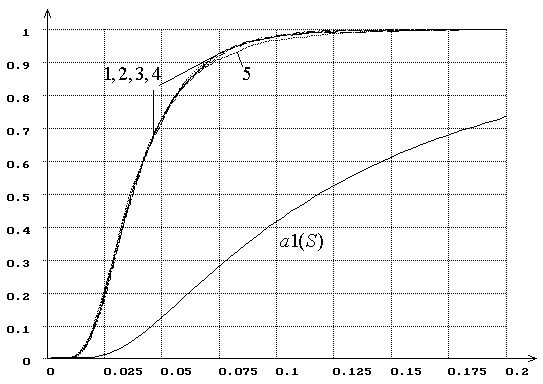
Рис. 13. Распределения ![]() статистики критерия типа
статистики критерия типа ![]() Мизеса
Мизеса ![]() при
оценивании двух параметров закона, соответствующего гипотезе
при
оценивании двух параметров закона, соответствующего гипотезе ![]() (1 – нормального, 2 – логистического, 3 –
Лапласа, 4 – наименьшего значения, 5 – Коши). При MD-оценках
(1 – нормального, 2 – логистического, 3 –
Лапласа, 4 – наименьшего значения, 5 – Коши). При MD-оценках ![]() .
.
При использовании MD-оценок,
минимизирующих по параметрам статистику ![]() ,
эмпирические распределения смоделированных распределений
,
эмпирические распределения смоделированных распределений ![]() практически совпадают для законов нормального,
логистического, Лапласа, наименьшего значения, максимального значения с
плотностью
практически совпадают для законов нормального,
логистического, Лапласа, наименьшего значения, максимального значения с
плотностью 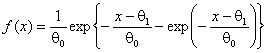 , распределения Вейбулла с плотностью
, распределения Вейбулла с плотностью 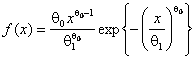 и хорошо аппроксимируются логарифмически
нормальным законом с плотностью
и хорошо аппроксимируются логарифмически
нормальным законом с плотностью ![]() и
параметрами
и
параметрами ![]() ,
, ![]() .
.
На рис. 14 представлены распределения ![]() статистики
типа
статистики
типа ![]() Мизеса
Мизеса ![]() при
использовании MD-оценок
при
использовании MD-оценок ![]() и оценивании масштабного параметра закона,
соответствующего гипотезе
и оценивании масштабного параметра закона,
соответствующего гипотезе ![]() (1
– нормального, 2 – логистического, 3 – Лапласа, 4 – наименьшего значения, 5 –
Коши, 6 – максимального значения, 7 – Вейбулла при оценивании параметра
формы). На рис. 15 представлены аналогичные распределения статистик при
оценивании параметра сдвига тех же распределений, что и на рис. 14.
Распределения статистик в случае оценивания параметра сдвига распределения
максимального значения и масштабного параметра распределения Вейбулла совпадают
с распределением статистики для распределения минимального значения.
(1
– нормального, 2 – логистического, 3 – Лапласа, 4 – наименьшего значения, 5 –
Коши, 6 – максимального значения, 7 – Вейбулла при оценивании параметра
формы). На рис. 15 представлены аналогичные распределения статистик при
оценивании параметра сдвига тех же распределений, что и на рис. 14.
Распределения статистик в случае оценивания параметра сдвига распределения
максимального значения и масштабного параметра распределения Вейбулла совпадают
с распределением статистики для распределения минимального значения.
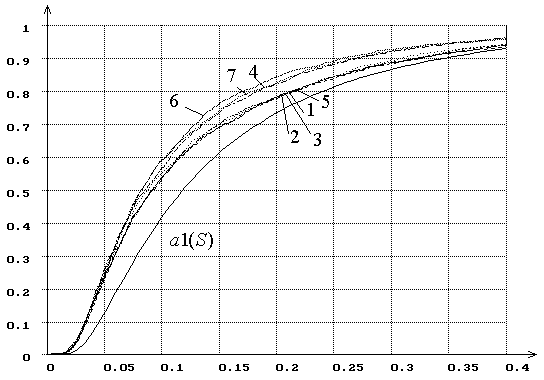
Рис. 14. Распределения ![]() статистики критерия типа
статистики критерия типа ![]() Мизеса
Мизеса ![]() при
оценивании масштабного параметра закона, соответствующего гипотезе
при
оценивании масштабного параметра закона, соответствующего гипотезе ![]() (1 – нормального, 2 – логистического, 3 –
Лапласа, 4 – наименьшего значения, 5 – Коши, 6 –максимального значения, 7 –
Вейбулла, параметр формы). При использовании MD-оценок
(1 – нормального, 2 – логистического, 3 –
Лапласа, 4 – наименьшего значения, 5 – Коши, 6 –максимального значения, 7 –
Вейбулла, параметр формы). При использовании MD-оценок ![]() .
.
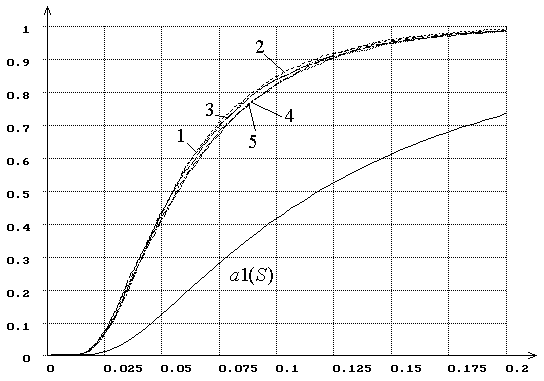
Рис. 15. Распределения ![]() статистики критерия типа
статистики критерия типа ![]() Мизеса
Мизеса ![]() при
оценивании параметра сдвига, соответствующего гипотезе
при
оценивании параметра сдвига, соответствующего гипотезе ![]() (1 – нормального, 2 – логистического, 3 –
Лапласа, 4 – наименьшего значения, 5 – Коши). При MD-оценках
(1 – нормального, 2 – логистического, 3 –
Лапласа, 4 – наименьшего значения, 5 – Коши). При MD-оценках ![]() .
.
Если обратить внимание на рис. 16, на котором
отображены распределения ![]() статистики
статистики
![]() при проверке согласия с распределениями
экспоненциальным
при проверке согласия с распределениями
экспоненциальным ![]() , полунормального
, полунормального ![]() , Рэлея
, Рэлея ![]() ,
Максвелла
,
Максвелла 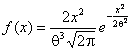 , модуля
, модуля ![]() -мерного
(
-мерного
(![]() ) нормального вектора
) нормального вектора ![]() при оценивании масштабного параметра
соответствующего закона с использованием MD-оценок
при оценивании масштабного параметра
соответствующего закона с использованием MD-оценок ![]() ,
то заметим, что распределения статистик близки к приведенным на рис. 15.
Распределения статистик, приведенные на рис. 16 достаточно хорошо
аппроксимируются логарифмически нормальным законом с параметрами
,
то заметим, что распределения статистик близки к приведенным на рис. 15.
Распределения статистик, приведенные на рис. 16 достаточно хорошо
аппроксимируются логарифмически нормальным законом с параметрами ![]() ,
, ![]() .
.
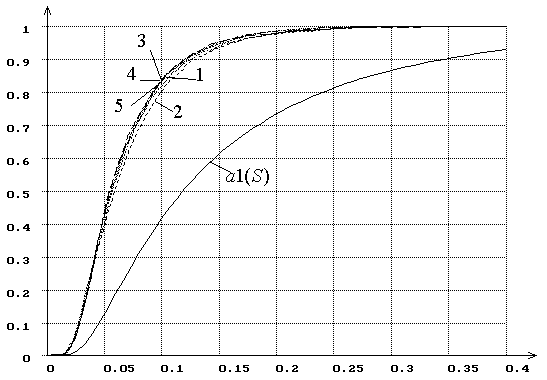
Рис. 16. Распределения ![]() статистики критерия типа
статистики критерия типа ![]() Мизеса
Мизеса ![]() при
оценивании масштабного параметра закона, соответствующего гипотезе
при
оценивании масштабного параметра закона, соответствующего гипотезе ![]() (1 – экспоненциального, 2 – полунормального, 3
– Рэлея, 4 – Максвелла, 5 – модуля 5-мерного нормального вектора). При
использовании MD-оценок
(1 – экспоненциального, 2 – полунормального, 3
– Рэлея, 4 – Максвелла, 5 – модуля 5-мерного нормального вектора). При
использовании MD-оценок ![]() .
.
Метод оценивания и мощность непараметрических критериев согласия
При использовании MD-оценок,
минимизирующих статистику критерия, эмпирические распределения ![]() , соответствующие различным гипотезам
, соответствующие различным гипотезам ![]() , имеют минимальный разброс, что позволяет говорить об
определенной «свободе от распределения» критериев. Если опираться только на
этот факт, то казалось бы, что только такие методы оценивания и следует применять
при проверке сложных гипотез. Но если исследовать мощность рассматриваемых
критериев при различных методах оценивания, то оказывается, что максимальную
мощность непараметрические критерии при близких альтернативах имеют в случае
оценивания параметров методом максимального правдоподобия.
, имеют минимальный разброс, что позволяет говорить об
определенной «свободе от распределения» критериев. Если опираться только на
этот факт, то казалось бы, что только такие методы оценивания и следует применять
при проверке сложных гипотез. Но если исследовать мощность рассматриваемых
критериев при различных методах оценивания, то оказывается, что максимальную
мощность непараметрические критерии при близких альтернативах имеют в случае
оценивания параметров методом максимального правдоподобия.
Рис. 17 иллюстрирует зависимость от ![]() распределений
распределений ![]() статистики
статистики ![]() критерия
типа Колмогорова при проверке сложной гипотезы при паре альтернатив
критерия
типа Колмогорова при проверке сложной гипотезы при паре альтернатив ![]() - нормальное распределение,
- нормальное распределение, ![]() - логистическое и использовании MD-оценок
- логистическое и использовании MD-оценок ![]() при
объеме выборок
при
объеме выборок ![]() = 20, 100, 500, 1000.
= 20, 100, 500, 1000.
Рис. 18 таким же образом характеризует зависимость от ![]() распределений
распределений ![]() статистики
статистики ![]() критерия
типа
критерия
типа ![]() Мизеса при проверке сложной гипотезы и
тех же альтернативах
Мизеса при проверке сложной гипотезы и
тех же альтернативах ![]() и
и
![]() при использовании MD-оценок
при использовании MD-оценок ![]() и
и
![]() = 100, 500, 1000.
= 100, 500, 1000.
Сравнивая рис. 17 с рис. 6, а рис. 18 с рис. 8, можем
убедиться, что в случае использования метода максимального правдоподобия
мощность критериев типа Колмогорова и типа ![]() Мизеса
много выше, чем при использовании соответствующих MD-оценок. Аналогичная картина справедлива и для
критерия типа
Мизеса
много выше, чем при использовании соответствующих MD-оценок. Аналогичная картина справедлива и для
критерия типа ![]() Мизеса со статистикой
Мизеса со статистикой ![]() Андерсона-Дарлинга.
Андерсона-Дарлинга.
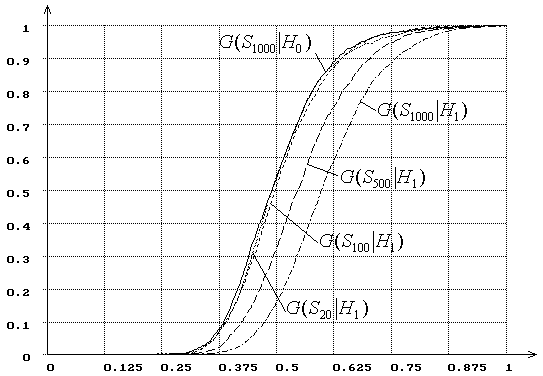
Рис. 17. Зависимость от ![]() распределений
распределений ![]() статистики критерия типа Колмогорова
статистики критерия типа Колмогорова ![]() при сложной гипотезе (
при сложной гипотезе (![]() - нормальное распределение,
- нормальное распределение, ![]() - логистическое, MD-оценки
- логистическое, MD-оценки ![]() ):
):
![]() = 20, 100, 500, 1000.
= 20, 100, 500, 1000.
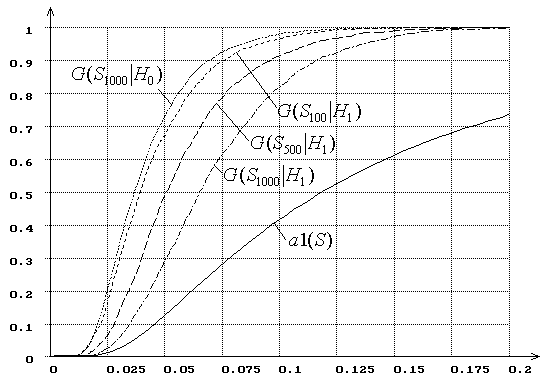
Рис. 18. Зависимость от ![]() распределений
распределений ![]() статистики критерия типа
статистики критерия типа ![]() Мизеса
Мизеса ![]() при
сложной гипотезе (
при
сложной гипотезе (![]() - нормальное распределение,
- нормальное распределение, ![]() - логистическое, MD-оценки
- логистическое, MD-оценки ![]() ):
):
![]() = 100, 500, 1000.
= 100, 500, 1000.
Для того чтобы сравнить по мощности непараметрические
критерии согласия для рассматриваемой пары близких гипотез ![]() и
и ![]() при
использовании ОМП на рис. 19 приведены распределения
при
использовании ОМП на рис. 19 приведены распределения ![]() и
и ![]() при
при
![]() = 20, 100, 500, 1000 для статистики
= 20, 100, 500, 1000 для статистики ![]() , а на рис. 20 для статистики
, а на рис. 20 для статистики ![]() критерия типа Смирнова. Анализируя распределения
на рисунках 6, 8, 19 и 20, можно заметить, что наиболее мощным для данной пары
гипотез является критерий типа
критерия типа Смирнова. Анализируя распределения
на рисунках 6, 8, 19 и 20, можно заметить, что наиболее мощным для данной пары
гипотез является критерий типа ![]() Мизеса
со статистикой
Мизеса
со статистикой ![]() , затем критерий типа
, затем критерий типа ![]() Мизеса со статистикой
Мизеса со статистикой ![]() , далее критерий типа Колмогорова со статистикой
, далее критерий типа Колмогорова со статистикой ![]() и на последнем месте критерий типа Смирнова со
статистикой
и на последнем месте критерий типа Смирнова со
статистикой ![]() . Данное наблюдение о порядке предпочтения критериев
хорошо согласуется с опытом их применения.
. Данное наблюдение о порядке предпочтения критериев
хорошо согласуется с опытом их применения.
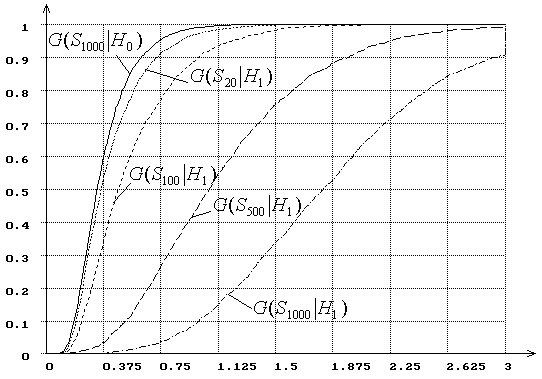
Рис. 19. Зависимость от ![]() распределений
распределений ![]() статистики критерия типа
статистики критерия типа ![]() Мизеса
Мизеса ![]() Андерсона-Дарлинга
при сложной гипотезе (
Андерсона-Дарлинга
при сложной гипотезе (![]() -
нормальное распределение,
-
нормальное распределение, ![]() -
логистическое, ОМП):
-
логистическое, ОМП): ![]() =
20, 100, 500, 1000.
=
20, 100, 500, 1000.
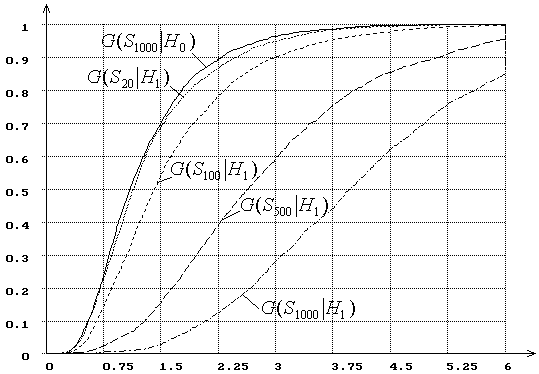
Рис. 20. Зависимость от ![]() распределений
распределений ![]() статистики критерия типа Смирнова
статистики критерия типа Смирнова ![]() при сложной гипотезе (
при сложной гипотезе (![]() - нормальное распределение,
- нормальное распределение, ![]() - логистическое, ОМП):
- логистическое, ОМП):
![]() = 20, 100, 500, 1000.
= 20, 100, 500, 1000.
Интересно, что при проверке этих же, но простых
гипотез мощность критерия Колмогорова выше мощности критерия ![]() Мизеса.
Мизеса.
Почему мощность рассматриваемых критериев при проверке
близких гипотез в случае ОМП выше, чем при MD-оценках, достаточно логично объясняет следующая
версия. Использование MD-оценок,
минимизирующих статистику критерия, приводит к распределению ![]() с меньшим параметром масштаба (к более крутой
функции распределения), чем в случае ОМП. Но с другой стороны MD-оценки в отличие от ОМП являются робастными, они
менее чувствительны к малым отклонениям выборки от предполагаемого закона
распределения. Поэтому функция распределения
с меньшим параметром масштаба (к более крутой
функции распределения), чем в случае ОМП. Но с другой стороны MD-оценки в отличие от ОМП являются робастными, они
менее чувствительны к малым отклонениям выборки от предполагаемого закона
распределения. Поэтому функция распределения ![]() оказывается еще более крутой по отношению к
аналогичному распределению при использовании ОМП.
оказывается еще более крутой по отношению к
аналогичному распределению при использовании ОМП.
Методика компьютерного анализа статистических закономерностей
Очевидно, что бесконечное множество случайных величин, с которым мы можем столкнуться на практике, не может быть описано ограниченным подмножеством моделей законов распределений, наиболее часто используемых для описания реальных наблюдений в приложениях. Вообще говоря, любой исследователь для конкретной наблюдаемой величины может предложить (построить) свою параметрическую модель закона, наиболее адекватно, с его точки зрения, описывающего эту случайную величину. Естественно, после оценки по данной выборке параметров модели возникает необходимость проверки сложной гипотезы об адекватности выборочных наблюдений и построенного закона с использованием критериев согласия.
Понятно, что множество всех сложных гипотез бесконечно и заранее иметь
распределения ![]() для любой сложной гипотезы
для любой сложной гипотезы ![]() практически невозможно. Именно поэтому найденные
различным образом предельные распределения статистик непараметрических
критериев согласия представлены в литературе лишь для ограниченного ряда
распределений, наиболее часто используемых в приложениях, особенно в задачах
контроля качества и исследования надежности. Что же делать, если для описания
выборки используется закон распределения вероятностей
практически невозможно. Именно поэтому найденные
различным образом предельные распределения статистик непараметрических
критериев согласия представлены в литературе лишь для ограниченного ряда
распределений, наиболее часто используемых в приложениях, особенно в задачах
контроля качества и исследования надежности. Что же делать, если для описания
выборки используется закон распределения вероятностей ![]() и найдена оценка его параметра
и найдена оценка его параметра ![]() , а для проверки сложной гипотезы
, а для проверки сложной гипотезы ![]() :
: ![]() исследователю
неизвестно распределение
исследователю
неизвестно распределение ![]() статистики
соответствующего критерия согласия?
статистики
соответствующего критерия согласия?
Наиболее целесообразно, на наш взгляд, воспользоваться
методикой компьютерного анализа статистических закономерностей. Мы настойчиво
рекомендуем этот подход, хорошо зарекомендовавший себя в наших исследованиях.
Для этого следует в соответствии с законом ![]() смоделировать
смоделировать
![]() выборок того же объема
выборок того же объема ![]() , что и выборка, для которой необходимо проверить
гипотезу
, что и выборка, для которой необходимо проверить
гипотезу ![]() :
: ![]() .
Для каждой из
.
Для каждой из ![]() выборок вычислить оценки тех же параметров, а
затем значение статистики
выборок вычислить оценки тех же параметров, а
затем значение статистики ![]() соответствующего
критерия согласия. В результате получим выборку
соответствующего
критерия согласия. В результате получим выборку ![]() значений статистики с законом распределения
значений статистики с законом распределения ![]() для проверяемой гипотезы
для проверяемой гипотезы ![]() . По этой выборке при достаточно большом
. По этой выборке при достаточно большом ![]() можно построить достаточно гладкую эмпирическую
функцию распределения
можно построить достаточно гладкую эмпирическую
функцию распределения ![]() ,
которой можно непосредственно воспользоваться для вывода о том, следует ли
принимать гипотезу
,
которой можно непосредственно воспользоваться для вывода о том, следует ли
принимать гипотезу ![]() . А можно, при желании, по
. А можно, при желании, по ![]() построить приближенную аналитическую модель,
аппроксимирующую
построить приближенную аналитическую модель,
аппроксимирующую ![]() , и тогда уже, опираясь на эту модель, принимать
решение по поводу проверяемой гипотезы. Хорошей аналитической моделью для
, и тогда уже, опираясь на эту модель, принимать
решение по поводу проверяемой гипотезы. Хорошей аналитической моделью для ![]() может оказаться функция распределения одного из
знакомых законов, часто используемых в приложениях, как было получено в [14].
Во всяком случае, всегда можно, опираясь на ограниченное множество законов
распределения, построить модель в виде смеси законов [29-31].
может оказаться функция распределения одного из
знакомых законов, часто используемых в приложениях, как было получено в [14].
Во всяком случае, всегда можно, опираясь на ограниченное множество законов
распределения, построить модель в виде смеси законов [29-31].
Реализация такой процедуры компьютерного анализа распределения статистики в настоящий момент не содержит ни принципиальных, ни практических трудностей. Уровень вычислительной техники позволяет очень быстро получить результаты моделирования, а реализация алгоритма под силу инженеру, владеющему навыками программирования. По крайней мере, применение методики не вызывает особых затруднений у студентов факультета прикладной математики и информатики.
Вместе с тем нельзя не согласиться с тем, что такая методика анализа распределений статистик имеет и недостатки, связанные с ограниченной точностью построения закона распределения статистики и возможным влиянием качества используемого датчика псевдослучайных чисел, о чем предупреждает А.И. Орлов [32]. Поэтому при ее реализации обязательно следует контролировать, как в нашем случае, качество датчиков, генерирующих числа в соответствии с требуемыми законами «наблюдаемых» случайных величин.
Отдельно следует коснуться точности построения закона
распределения статистики на основании ![]() .
Конечно, точность можно повышать, увеличивая
.
Конечно, точность можно повышать, увеличивая ![]() . По нашим оценкам отклонения смоделированного
распределения от теоретического при
. По нашим оценкам отклонения смоделированного
распределения от теоретического при ![]() обычно
имеют порядок
обычно
имеют порядок ![]() . Если поставить такую цель, то, аппроксимируя эмпирические
распределения теоретическими законами и усредняя их по реализациям (при
многократном моделировании), можно при необходимости добиться более высокой
точности построения закона распределения исследуемой статистики. Вопрос только
в том, есть ли в этом необходимость. Как видим, опираясь на построенное
распределение
. Если поставить такую цель, то, аппроксимируя эмпирические
распределения теоретическими законами и усредняя их по реализациям (при
многократном моделировании), можно при необходимости добиться более высокой
точности построения закона распределения исследуемой статистики. Вопрос только
в том, есть ли в этом необходимость. Как видим, опираясь на построенное
распределение ![]() , можно достаточно точно оценить величину
, можно достаточно точно оценить величину ![]() , но значения процентных точек, полученные по
, но значения процентных точек, полученные по ![]() , могут оказаться с существенной погрешностью. На
практике же, к сожалению, проверяя различные гипотезы, чаще сравнивают
полученное значение статистики
, могут оказаться с существенной погрешностью. На
практике же, к сожалению, проверяя различные гипотезы, чаще сравнивают
полученное значение статистики ![]() с
соответствующей процентной точкой предельного распределения, от чего, по нашему
мнению, давно следует отказаться и принимать решение по достигнутому уровню
значимости
с
соответствующей процентной точкой предельного распределения, от чего, по нашему
мнению, давно следует отказаться и принимать решение по достигнутому уровню
значимости ![]() .
.
Выводы
Таким образом, на основании проведенных исследований можно сделать следующие выводы и рекомендации.
Распределения статистик непараметрических
критериев согласия при простых и сложных гипотезах очень быстро сходятся к
предельным законам. Уже при ![]() ,
не опасаясь больших ошибок, можно пользоваться этими предельными законами для
вычисления достигаемого уровня значимости
,
не опасаясь больших ошибок, можно пользоваться этими предельными законами для
вычисления достигаемого уровня значимости ![]() .
.
В то же время, следует иметь ввиду, что различать близкие гипотезы (особенно простые) при малых выборках с помощью непараметрических критериев согласия невозможно.
Мощность
непараметрических критериев при проверке сложных гипотез при тех же объемах
выборок ![]() всегда существенно выше, чем при
проверке простых.
всегда существенно выше, чем при
проверке простых.
Следует помнить,
что при проверке сложных гипотез, распределения статистик ![]() непараметрических критериев
зависят не только от закона распределения
непараметрических критериев
зависят не только от закона распределения ![]() ,
соответствующего гипотезе
,
соответствующего гипотезе ![]() , числа и вида
оцениваемых параметров (иногда, конкретного значения параметра), но и от
используемого метода оценивания параметров. Ни в коем случае нельзя
использовать (предельный) закон распределения статистики, построенный для
одного метода оценивания, применяя другой.
, числа и вида
оцениваемых параметров (иногда, конкретного значения параметра), но и от
используемого метода оценивания параметров. Ни в коем случае нельзя
использовать (предельный) закон распределения статистики, построенный для
одного метода оценивания, применяя другой.
В случае
применения MD-оценок, минимизирующих статистику критерия,
распределения статистик непараметрических критериев в меньшей степени
подвержены зависимости от вида ![]() ,
соответствующего гипотезе
,
соответствующего гипотезе ![]() . Однако,
наиболее мощными эти критерии оказываются при использовании ОМП.
. Однако,
наиболее мощными эти критерии оказываются при использовании ОМП.
В случае простых
гипотез и близких альтернативах непараметрические критерии согласия уступают по
мощности критериям типа ![]() . В случае
проверки сложных гипотез – преимущество за непараметрическими критериями
согласия. В то же время, мы рекомендуем при проверке гипотез о согласии не
останавливаться на использовании одного из критериев согласия, так как каждый
из критериев по-разному улавливает различные отклонения эмпирического распределения
от теоретического.
. В случае
проверки сложных гипотез – преимущество за непараметрическими критериями
согласия. В то же время, мы рекомендуем при проверке гипотез о согласии не
останавливаться на использовании одного из критериев согласия, так как каждый
из критериев по-разному улавливает различные отклонения эмпирического распределения
от теоретического.
Изложенная и апробированная методика моделирования распределений статистик при корректном ее применении может быть рекомендована для построения статистических закономерностей в ситуации, когда аналитическими методами не удается решить задачу.
ЛИТЕРАТУРА
1.
Kac
M., Kiefer J., Wolfowitz J. On tests of normality and other tests of goodness
of fit based on distance methods // Ann. Math. Stat., 1955. V.26. - P.189-211.
2. Durbin J. Kolmogoriv-Smirnov test when parameters are estimated // Lect. Notes Math. 1976. V. 566. P. 33-44.
3. Мартынов Г.В. Критерии омега-квадрат. – М.: Наука, 1978. – 80 с.
4.
Pearson E.S., Hartley H.O. Biometrica tables for Statistics.
V.2. – Cambridge: University Press, 1972. – 634 p.
5.
Stephens M.A. Use of Kolmogorov-Smirnov, Cramer - von
Mises and related statistics – vithout extensive table // J. R. Stat. Soc.,
1970, B. 32. – P. 115-122.
6.
Stephens M.A. EDF statistics for goodness of fit and
some comparisons // J. Am. Statist. Assoc., 1974, v.69. – P. 730-737.
7. Chandra M., Singpurwalla N.D., Stephens M.A. Statistics for Test of Fit for the Extrem-Value and Weibull Distribution // J. Am. Statist. Assoc., 1981, v.76. – P. 375.
8. Тюрин Ю.Н. О предельном распределении статистик Колмогорова-Смирнова для сложной гипотезы // Изв. АН СССР. Сер. Матем., 1984, т. 48, № 6. – C. 1314-1343.
9. Тюрин Ю.Н., Саввушкина Н.Е. Критерии согласия для распределения Вейбулла-Гнеденко. // Изв. АН СССР. Сер. Техн. кибернетика, 1984, № 3. – C. 109-112.
10. Тюрин Ю.Н. Исследования по непараметрической статистике (непараметрические методы и линейная модель). Автореф. дисс. на соиск. учен. степени д-ра физ.-мат. наук. – М., 1985. - 33 с. – (МГУ).
11. Саввушкина Н.Е. Критерий Колмогорова-Смирнова для логистического и гамма-распределения // Сб. тр. ВНИИ систем. исслед. – 1990, № 8.
12. Тюрин Ю.Н., Макаров А.А. Анализ данных на компьютере. // М.: ИНФРА-М, Финансы и статистика, 1995. – 384 с.
13. Лемешко Б.Ю., Постовалов С.Н. Прикладные аспекты использования критериев согласия в случае проверки сложных гипотез // Надежность и контроль качества. 1997. – № 11. – С. 3-17.
14. Лемешко Б.Ю., Постовалов С.Н. О распределениях статистик непараметрических критериев согласия при оценивании по выборкам параметров наблюдаемых законов // Заводская лаборатория. 1998. – № 3. – С. 61-72.
15. Орлов А.И. Распространенная ошибка при использовании критериев Колмогорова и омега-квадрат // Заводская лаборатория, 1985. Т. 51. №1. - С. 60-62.
16. Бондарев Б.В. О проверке сложных статистических гипотез // Заводская лаборатория. 1986. Т. 52. № 10. - С. 62-63.
17. Кулинская Е.В., Саввушкина Н.Е. О некоторых ошибках в реализации и применении непараметрических методов в пакете для IBM PC // Заводская лаборатория, 1990. Т. 56. № 5. - С. 96-99.
18. Лемешко Б.Ю., Постовалов С.Н. Исследование допредельных распределений статистик критериев согласия при проверке сложных гипотез // Тр. IV международной конференции “Актуальные проблемы электронного приборостроения”. Новосибирск, 1998. Т.3. – С. 12-16.
19. Орлов А.И. О критериях Колмогорова и Смирнова //
Заводская лаборатория. 1995. Т. 61. № 7. С. 59-61.
20. Kolmogoroff A.N. Sulla determinazione empirica di una legge di distribuzione. // G. Ist. Ital. attuar., 1933, vol. 4., № 1. – P. 83-91.
21. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. - М.: Наука, 1983. - 416 с.
22. Орлов А.И. Неустойчивость параметрических методов отбраковки резко выделяющихся наблюдений // Заводская лаборатория. 1992. Т. 58. № 7. С. 40-42.
23. Денисов В.И., Лемешко Б.Ю., Цой Е.Б. Оптимальное группирование, оценка параметров и планирование регрессионных экспериментов: В 2 ч. / Новосиб. гос. техн. ун-т. - Новосибирск, 1993. - 346 с.
24. Лемешко Б.Ю. Асимптотически оптимальное группирование наблюдений - это обеспечение максимальной мощности критериев // Надежность и контроль качества. - 1997. - № 8. - С. 3-14.
25.
Лемешко Б.Ю. Асимптотически оптимальное
группирование наблюдений в критериях согласия // Заводская лаборатория,
1998. Т.
64. – №1. – С. 56-64.
26. Rao C.R. Criteria
of estimation in large samples // Sankhua, 1962. - V. 25. - P. 189-206.
27. Рао С.Р. Линейные статистические методы и их применения. - М.: Наука, 1968. - 548 с.
28. Орлов А.И. О нецелесообразности использования итеративных процедур нахождения оценок максимального правдоподобия // Заводская лаборатория. 1986. Т. 52. № 5. С. 67-69.
29. Лемешко Б.Ю., Постовалов С.Н. Статистический анализ одномерных наблюдений по частично группированным данным // Изв. вузов. Физика. - Томск, 1995. - № 9. - С. 39-45.
30. Лемешко Б.Ю., Постовалов С.Н. Статистический анализ смесей распределений по частично группированным данным // Сб. научных трудов НГТУ. - Новосибирск: изд-во НГТУ. 1995. - №1. -С. 25-31.
31. Лемешко Б.Ю., Постовалов С.Н. Вопросы обработки выборок одномерных случайных величин // Научный вестник НГТУ. - Новосибирск, 1996. № 2. - C. 3-24.
32. Орлов А.И. Методы оценки близости допредельных и предельных распределений статистик // Заводская лаборатория. 1998. Т. 64. – № 5. – С. 64-67.