См. также: Прикладная математическая статистика (материалы к семинарам)

 

Заводская лаборатория. Диагностика материалов. 2001. Т. 67. - № 3. - С. 52-58.

 

УДК 519.2

 

О РАСПРЕДЕЛЕНИЯХ СТАТИСТИКИ И МОЩНОСТИ КРИТЕРИЯ ТИПА  НИКУЛИНА

 

Б.Ю. Лемешко, С.Н. Постовалов, Е.В. Чимитова

 

            С использованием критериев согласия могут проверяться простые ги­потезы вида : , где  – функция распределения веро­ятностей, с которой проверяется согласие наблюдаемой выборки неза­виси­мых одинаково распределенных величин , а  – известное значение параметра (скалярного или векторного), и сложные гипотезы : , где  – пространство параметров. В процессе проверки сложной гипотезы оценка параметра  вычисляется по этой же самой выборке. Если оценка  вычислена по другой выборке, то гипотеза про­стая.

            При использовании критериев согласия типа  область определения случайной величины разбивается на  интервалов граничными точками

.

            Статистика  Пирсона вычисляется в соответствии с соотношением

,                                       (1)

где  – количество наблюдений, попавших в интервал,  – вероятность попадания наблюдения в -й интервал, , . При справед­ливой простой гипотезе  пре­дельное распределение статис­тики  есть -распределение с числом сте­пеней свободы . Если по выборке оценивалось  параметров за­кона в результате мини­мизации ста­тистики , статистика подчиняется -распределению с  степенями свободы. При справедливой альтернативной гипотезе  пре­дельное рас­пределение  пред­ставляет собой нецентральное -распределение с тем же числом степеней свободы и параметром нецен­тральности

.                                       (2)

            В случае проверки сложных гипотез и оценивании по выборке пара­метров наблюдаемого закона использо­вание в качестве пре­дельных -распре­делений справедливо лишь при опре­делении оценок минимизацией статистики  [1] или при вычислении по сгруп­пи­рован­ным данным оценок максимального правдоподобия (ОМП).

Если при проверке такой сложной гипотезы используются ОМП по негруп­пированным данным, то эта же статистика распределена в пределе как сумма независимых сла­га­емых , где  - стандартные нормальные слу­чай­ные вели­чины, независимые между собой и с . Величины  – не­кото­рые числа между 0 и 1 [2-3], представляющие собой корни уравнения

 ,                                    (3)

где  – информационная матрица Фишера по негруппированным дан­ным, соответствующая одному наблюдению,

,                    (4)

а  – по группированным

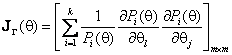.                                (5)

            В работе [4] распределения  этой статистики при проверке сложных гипотез были исследованы методами компьютерного моделиро­вания в зависимости от способа группирования наблюдений (от способа разбиения области определения на интервалы). Было показано, что при ис­пользовании асимпто­тически оптимального группирования, при котором минимизируются потери в информации Фишера [5-8], например, максими­зируется определитель  матрицы , зависящей от граничных точек ин­тервалов, распределения  в области больших значений статис­тики настолько близки к со­ответству­ющим -распре­делениям, что по­следними можно пользо­ваться без опасения совершить большую ошибку при вычислении вероятности вида , где  - значение статис­тики, вычис­ленное по вы­бор­ке. Однако в общем случае условные распреде­ления статистики  су­щес­твенно отличаются от -распре­де­лений. И для корректного приме­нения кри­терия согласия желательно более точное знание предельного распределения статистики.

В работах [9-12] Никулиным предлагается такое видоизменение стан­дар­т­ной статистики , при котором предельное распределение есть обыч­ное распределение  (количество степеней свободы не зависит от числа оцениваемых параметров). Неизвестные параметры распределения  в этом случае должны оцениваться по негруппированным данным методом максимального правдоподобия. При этом вектор вероятностей попадания в интервал  предпо­ла­га­ется заданным и граничные точки ин­тер­валов определяются соот­­ноше­ниями , .

Предложенная статис­тика отличается от  только при сложных ги­потезах и имеет вид [10]

,                               (6)

где  вычисляется в соответствии с (1). Элементы и размерность матрицы

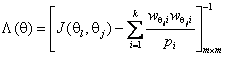                                (7)

определяются оцениваемыми компонен­тами вектора параметров ,  - эле­менты информационной матри­цы ,  - элементы вектора , величины  определяются соотношением

.                     (8)

            Несложно показать, что для законов , определяемых только двумя параметрами сдвига и масштаба, справедливо соотношение

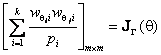                                         (9)

и, следовательно,

.                                    (10)

            Действительно, для законов с параметром сдвига  и масштаба  с функцией распределения  и плотностью  эле­менты информационной матрицы  имеют вид:

,

 ,

,

где . Тогда нетрудно заметить, что

, 

.

            С момента публикации работ [9-10] прошло более 25 лет, но, не счи­тая работ самого Никулина, нам не известны публикации других авторов, посвященные этой статистике, и, тем более, какие-либо упоминания о ре­зультатах использования статистики  в приложениях.

            Целью настоящей работы явилось стремление проверить, насколько хорошо распределение статистики  при справедливой нулевой гипотезе  соответствует распределению , а, во-вторых, сравнить мощ­ность предложенного Никулиным критерия с мощностью критерия  Пирсона. Основанием для проведения исследований послужили следующие соображения. С одной стороны, как уже говорилось, при вычислении ОМП по негруппированным наблюдениям, и использовании асимптотически оп­тимального группирования распределения  в области больших значений статистики достаточно близки к -распре­делениям [4]. С другой стороны, очевидно, что вычисление статистики  сопряжено с несколько большими вычислительными (и аналитическими) затратами. Следовательно, для того, чтобы рекомендовать её применение, необходимо указать конкретные преимущества, связанные с этой статистикой и показы­вающие, что использование статистики  не хуже в каком-то смысле. На­пример, что при близких альтернативах, как показано в [9,11,12], мощность критерия Никулина действительно не меньше мощности критерия Пирсона.

            В данной работе, как и в [4,8,13], нами использована методика ком­пьютерного анализа статистических закономерностей, которая позволяет с достаточной для практических задач точностью моделировать законы рас­пределения исследуемых статистик. Эмпирические функции смоделированных распределений статистик, приводимые в статье, строились при объемах выборок статистик . Полученные результаты для наглядности иллюстрируются на приводимых рисунках без сглаживания эмпирических распределений аппроксимирующими зависимостями. С одной стороны это позволяет проследить реальные закономерности, с другой – судить о точ­ности построения соответствующих функций распределения. Естественно, что такая методика анализа допредельных и предельных распределений статистик, как справедливо отмечает А.И. Орлов [14], имеет свои недостатки, связанные с ограниченной точностью построения закона распределения статистики и влиянием качества используемого датчика псевдослучайных чисел. В нашем случае качество датчиков, генерирующих числа в соответствии с заданными законами «наблюдаемых» случайных величин, контролировалась с использованием программной системы [15]. По нашим оценкам отклонения смоделированного распределения от теоретического при  обычно имеют порядок . Об этом же позволяет судить и степень совпадения моделируемых распределений классических статистик с их известными предельными законами распределения.

Как показано в [4], распределения  существенно зависят от способа группирования выборки. В частности, эти распределения заметно отличаются при разбие­нии выборки на равновероятные и асимптотически оптимальные интер­валы. Ещё в большей степени способ группирования отражается на распре­делениях  и, следовательно, на мощности критерия Пирсона: при близких альтернативах и асимптотически оптимальном группировании его мощность максимальна.

            Исследование методами компьютерного моделирования распределе­ний  показало, что на эти распределения способы группи­рования практически не влияют: и при равновероятном (РВГ), и при асимпто­тиче­ски оптимальном (АОГ) группировании распределения  хорошо согла­су­ются с -распре­делением. Например, на рис. 1 показаны эмпири­ческие распределения  при проверке гипотезы о согласии с логис­тическим законом 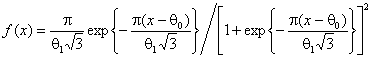 и вычисле­нии по выборке ОМП двух параметров этого распределения. Выборка разбивалась на 7 интервалов. И при равно­вероятном  и при асимпто­тически оптимальном группирова­нии  эмпирические распределения практически совпали с -распре­делением. Аналогичная картина наблюдается и при других нулевых гипотезах.

 

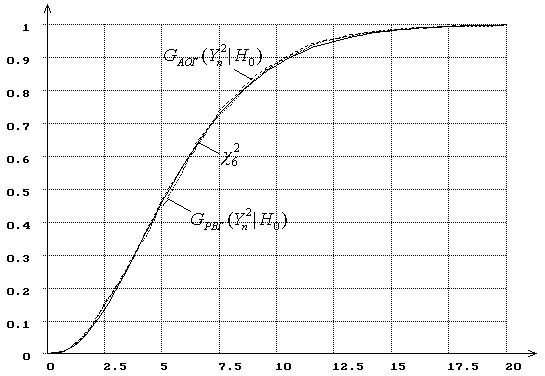
Рис.1. Распределения статистики  при оценивании двух параметров логистического распределения, соответствующего верной гипотезе .

 

На предельные распределения  способ группирования ока­зы­ва­ет заметное, но не сравнимо меньшее влияние, чем на распределения . Проведенные исследования показали, что различия между рас­пределениями  и  заметны, но не так существенны, как для аналогичных распределений статистики . При этом в боль­шинстве случаев кривая распределения  прохо­дит ниже, чем , что, вообще говоря, указывает на то, что, в отли­чие от кри­терия  Пирсона, критерий типа  Никулина несколько мощнее в случае равновероятного группирования(!). В табл. 1 приведены значения  мощности критериев типа  Пирсона () и Никулина () при проверке сложных гипотез с оцениванием двух параметров рас­пре­деления, соответ­ствующего гипотезе  при уровне значимости , объеме выборки , при числе ин­тервалов группирования . В первом случае ги­потезе  соот­ветствовало нормальное распределение 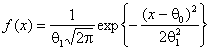, а гипотезе  – ло­гистическое. Во втором случае – наоборот.

 

Таблица 1.

 

Оценивались

: Нормальный закон

: Логистический закон

: Логистический закон

: Нормальный закон

параметры

 

АОГ

РВГ

АОГ

РВГ

АОГ

РВГ

АОГ

РВГ

Оба пара­метра

0.69

0.71

0.57

0.53

0.43

0.47

0.45

0.23

Сдвига

0.44

0.45

0.45

0.46

0.4

0.4

0.44

0.44

Масштаба

0.64

0.69

0.61

0.47

0.5

0.46

0.5

0.19

 

На рис. 2-4 представлены графики распределений статистик  и  при справедливой нулевой гипотезе ( и ), которая соот­ветствует нормаль­ному распределению, и при верной альтернативе ( и ), соответствующей логистическому закону. Услов­ные распределения статистик при справедливой альтернативе всюду строи­лись при объеме выборки . Распределения на рис. 2 соответствуют случаю, когда вычисляются ОМП двух параметров нормального распреде­ления, на рис. 3 – при вычислении ОМП только параметра сдвига, а на рис. 4 – при вычислении ОМП только параметра масштаба. На рис. 2 и после­дующих вертикальная линия от условного распределения при справедливой нулевой гипотезе  до условного распределения, соответствующего вер­ной альтер­нативе , позволяет ориентироваться в значениях мощности при уровне значимости : ордината её нижнего конца определяет ошибку второго рода .

 

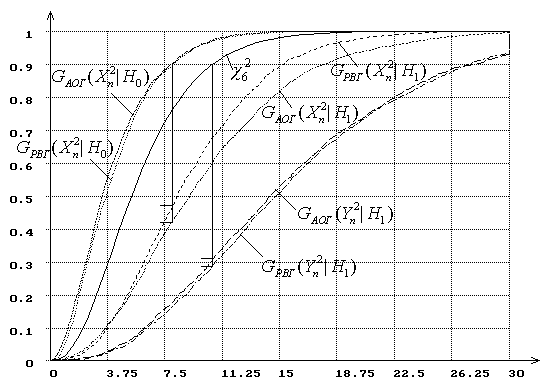
Рис. 2. Распределения статистик  и  при вычислении ОМП двух параметров нормального распределения (: нормальный закон, : логистический).

 

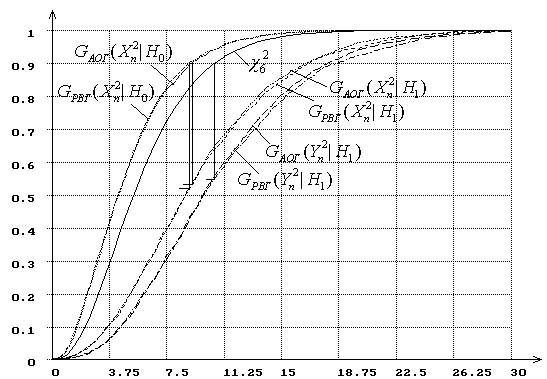
Рис. 3. Распределения статистик  и  при вычислении ОМП параметра сдвига нормального распределения

 

 (: нормальный закон, : логистический).

 

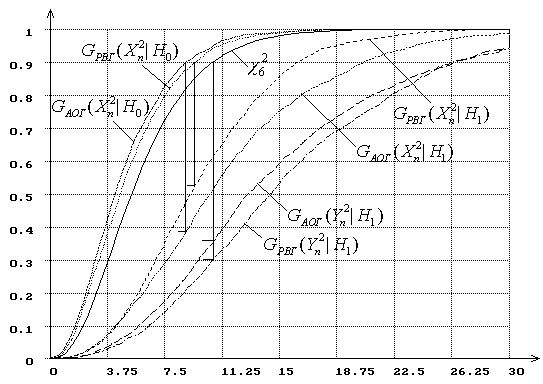
Рис. 4. Распределения статистик  и  при вычислении ОМП параметра масштаба  нормального распределения

 

 (: нормальный закон, : логистический).

 

Как следует из результатов, представленных в табл. 1 и на рис. 2-4, мощность критерия типа  Никулина с использованием статистики  при различении близких гипотез, каковыми являются нормальное и логи­стическое распределения, не хуже, чем в этой же ситуации (при проверке сложной гипотезы) мощность критерия типа  Пирсона с использованием статистики  с применением асимптоти­чески оптимального группирова­ния. Необхо­димо особо отметить, что группирование, при котором мини­мизи­руются потери в информации Фишера и при котором критерий типа  Пирсона лучше всего различает близкие гипотезы, уже не является оп­тимальным в этом смысле для критерия Никулина: при равновероятном группировании этот критерий обычно оказывается мощнее.

Сравним по мощности рассматриваемые критерии с непараметричес­кими критериями типа Колмогорова и типа  Мизеса при проверке сложной гипотезы в полностью аналогичной ситуации: по выборке вычисляются ОМП двух параметров нормального распределения,  соответствует нормальному закону,  – логистическому, объём выборки .

На рис. 5 представлены распре­деления  и  статис­ти­ки типа Колмогорова, имеющей вид [16]

,

где  

 - объем выборки,  - упорядоченные по возрастанию вы­бо­роч­ные значения,  - функция закона распределения, согласие с которым про­веряется. А на рис. 6 – распределения  и  статистики типа  Мизеса вида [16]

.

 

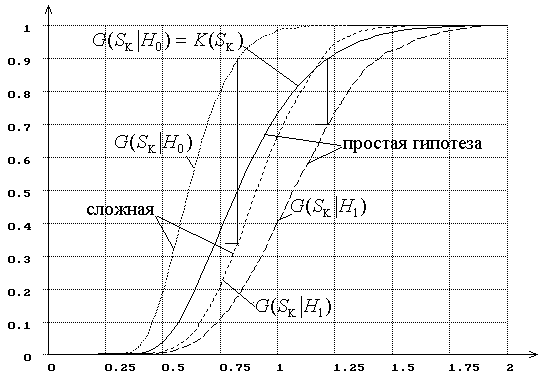
Рис.5. Распределения статистики критерия типа Колмогорова при проверке сложной гипотезы и вычислении ОМП двух параметров нормального распределения (: нормальный закон, : логистический) и при проверке простой гипотезы. – распределение Колмогорова.

 

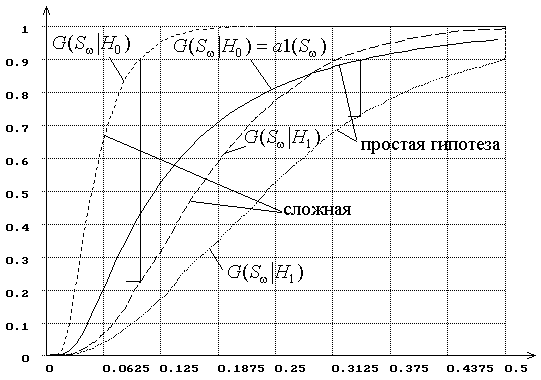
Рис. 6. Распределения статистики критерия типа  Мизеса при проверке сложной гипотезы и вычислении ОМП двух параметров нормального распределения (: нормальный закон, : логистический) и при проверке простой гипотезы.  – предельное распределение статистики при простой гипотезе.

 

Мощность критерия типа Колмогорова при уровне значимости  ока­зывается равной 0.66 (см. рис. 5), критерия типа  Мизеса – 0.775 (см. рис.6) (сравните с 0.71 для  и  0.53 для , рис. 2 и табл. 1).

            Если рассмотреть те же самые, но простые гипотезы  и , то мощность этих критериев при  составит величину: для критерия Кол­могорова – 0.3 (рис. 5), для критерия  Мизеса – 0.275 (рис. 6), для кри­терия  Пирсона – 0.43 при равновероятном группировании и 0.54 при асимп­тотически оптимальном (рис. 7).

 

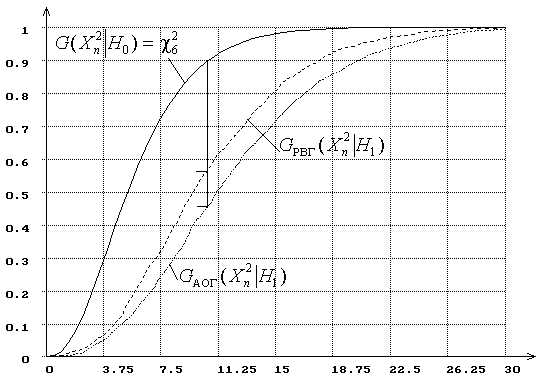
Рис.7. Распределения статистики  при проверке простой гипотезы

 

 

(: нормальный закон, : логистический, ).

 

            Применяя критерии типа  Пирсона, стараются разбить область определения случайной величины, по возможности, на большее число ин­тервалов. Конечно, в этом случае потери информации уменьшаются. Но интересно, что в этом случае происходит с мощностью критерия согласия. Об изменении мощности критерия с ростом числа интервалов для статис­тики  при проверке простой гипотезы можно судить по рис. 8, на кото­ром представлены распределения  и  для рассматри­ваемых гипотез  и  при числе интервалов  и объёме вы­борки . Для  на рисунке приведены  и . Ордината нижнего конца соответствующей вертикальной линии определяет величину  при уровне значимости . Как видим, в полном соответствии с результатами работ [17,18] при увеличении числа интервалов мощность критерия падает.

 

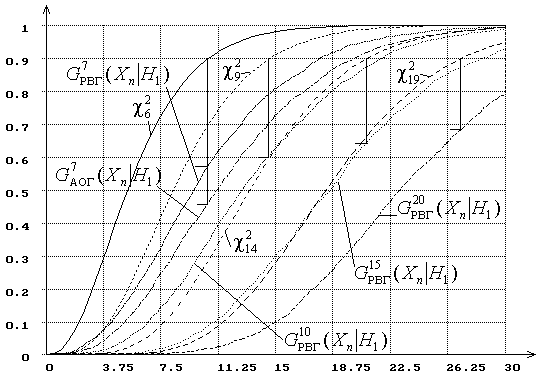
Рис.8. Распределения статистики  при проверке простой гипотезы

 

 

(: нормальный закон, : логистический, ).

 

            Аналогичные изменения мощности критерия для статистики  в за­висимости от числа интервалов при проверке сложной гипотезы иллюстри­рует рис. 9. И здесь с ростом  мощность критерия падает.

            А вот мощность критерия Никулина с использованием статистики  с ростом  уменьшается существенно медленней (см. рис. 10) и она выше, чем мощность критерия  Пирсона.

 

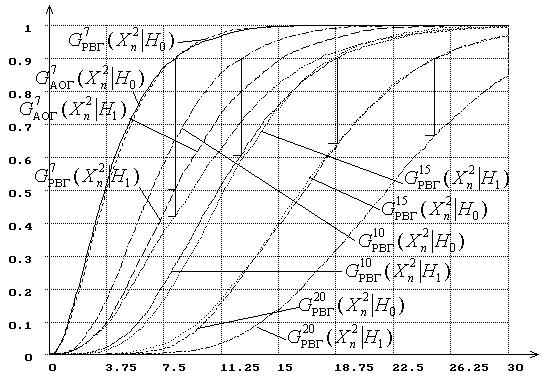
Рис.9. Распределения статистики  при проверке сложной гипотезы

 

 

(: нормальный закон, : логистический, ).

 

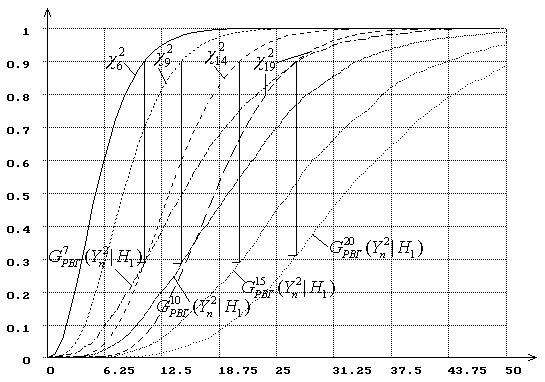
Рис.10. Распределения статистики  при проверке сложной гипотезы

 

 

(: нормальный закон, : логистический, ).

 

            В табл. 2 представлены значения мощности критериев  Пирсона и типа  Никулина в случае рассматриваемой пары альтернатив (: нормальный закон, : логистический) при различном числе интервалов  в случае простых и сложных гипотез. В колонке «2» приведены значения мощности критерия  Пирсона при проверке простой гипотезы, полученные по результатам моделирования. В колонке «3» приведены теоретические значения мощности, вычисленные при условии, что  представляет собой -распределение, а  – соответствующее нецентральное распределение. Колонка «4» содержит значения мощности критерия  Пирсона при проверке сложной гипотезы, полученные по результатам моделирования при использовании ОМП по негруппированным наблюдениям. В колонке «5» приведены теоретические значения мощности критерия  Пирсона при проверке сложной гипотезы, вычисленные при условии, что  представляет собой -распределение (оценки параметров вы­чис­ляются при минимизации статистики ), а  – соответствующее нецентральное распределение. В колонке «6» приведены значения мощности критерия Никулина, полученные в результате моде­лиро­вания распределений статистики , а в колонке «7» – расчетные значения мощности этой статистики при рассматриваемой паре гипотез  и .

 

Таблица 2.

Значения мощности критериев  Пирсона и типа  Никулина

при уровне значимости a=0.1

(: нормальный закон, : логистический закон)

 

 

 

 

В случае простой

 гипотезы

В случае сложной гипотезы

Для статистики

 =

Для статистики

Для статистики

 

По результатам моделиро­вания

 

 

Теорети­ческая

По результатам моделиро­вания (при использова­нии ОМП)

Теорети­ческая (при использова­нии оценок min)

 

По результатам моделиро­вания

 

 

Теорети­ческая

1

2

3

4

5

6

7

6

0.46

0.449

0.53

0.526

0.70

0.742

7

0.43

0.427

0.49

0.488

0.71

0.752

8

0.42

0.409

0.45

0.459

0.71

0.757

9

0.38

0.395

0.43

0.436

0.71

0.758

10

0.38

0.383

0.43

0.418

0.71

0.757

11

0.37

0.373

0.41

0.403

0.71

0.756

12

0.35

0.364

0.41

0.391

0.70

0.753

13

0.35

0.357

0.38

0.381

0.70

0.750

14

0.34

0.351

0.38

0.373

0.69

0.747

15

0.33

0.345

0.38

0.365

0.69

0.743

16

0.33

0.340

0.38

0.359

0.69

0.739

17

0.32

0.336

0.37

0.353

0.69

0.735

18

0.32

0.332

0.37

0.348

0.69

0.731

19

0.32

0.328

0.35

0.343

0.68

0.727

20

0.31

0.325

0.35

0.339

0.68

0.723

21

0.31

0.322

0.34

0.335

0.67

0.719

22

0.31

0.319

0.34

0.331

0.67

0.715

23

0.31

0.317

0.34

0.328

0.66

0.711

24

0.30

0.314

0.34

0.325

0.66

0.707

25

0.30

0.312

0.34

0.322

0.66

0.703

26

0.30

0.310

0.33

0.320

0.65

0.699

27

0.30

0.308

0.33

0.317

0.65

0.695

28

0.30

0.306

0.32

0.315

0.65

0.692

29

0.30

0.304

0.32

0.313

0.65

0.688

30

0.30

0.302

0.32

0.310

0.65

0.685

 

            В табл. 2 приводятся значения мощности критериев  от 6 до 30. Проследив изменение мощности критериев при <6, мы убедимся, что, если мощность критерия  Пирсона с уменьшением числа интервалов продолжает возрастать, то мощность критерия Никулина со статистикой  при  начинает падать. Об этом свидетельствуют как результаты моделирования распределений статистик, так теоретические расчеты мощности критериев. Следовательно, для критерия Никулина существует оптимальное число интервалов, при котором его мощность максимальна.

 

Выводы

 

Таким образом, проведенные исследования свойств статистики, пред­ложенной Никулиным, показали, что она обла­дает тремя важными для практического применения достоинствами.

Во-первых, при любой сложной проверяемой гипотезе  и использовании асимп­тотически эффективных ОМП па­раметров по исходной негруп­пирован­ной выборке статистика  при спра­вед­ливой гипотезе  имеет в качестве предельного известное точно рас­преде­ление . По существу, это уникальное свойство “свободы от рас­пределения” при проверке сложной гипотезы.

Во-вторых, распределения статистики  практически не зависят от способа группирования, спо­соба разбиения области определения случайной величины на интер­ва­лы.

В-тре­тьих, мощность критерия Никулина при близких альтернативах выше мощности кри­терия Пирсона. Это говорит о том, что с его помощью лучше различаются близкие гипотезы. 

Вышеперечисленное позволяет настойчиво рекомендовать при­ме­нение статистики  в приложениях и, особенно, для включения в про­граммное обеспечение задач статистиче­ского анализа. Некоторые допол­ни­тельные усилия при реализации, связан­ные с большей сложностью статистики  по сравнению со статистикой , в конечном счете, себя оправдывают.

Отметим попутно следующие, по нашему мнению, бесспорные факты, которые должны учитываться при проведении статистического ана­лиза. Во-первых, выбирая число интервалов в критериях типа , мы должны осознавать, что увеличение их числа не приводит к росту мощности критерия. Во-вторых, следует учитывать, что при проверке простых ги­потез непара­метрические критерии согласия уступают по мощности кри­териям типа , особенно, если в последних применяется асимпто­тически оптимальное груп­пирование [5-7]. В то же время, при проверке сложных гипотез непараметрические критерии оказываются более мощными. И в этом слу­чае критерий Никулина по мощности приближается к непараметрическим.

 

 

ЛИТЕРАТУРА

 

1.    Кендалл М., Стьюарт А. Статистические выводы и связи. – М.: Наука, 1973. – 900 с.

2.    Chernoff H., Lehmann E.L. The use of maximum likelihood estimates in  test for goodness of fit // Ann. Math. Stat., 1954. V. 25. – P. 579-586.

3.    Чибисов Д.М. Некоторые критерии типа хи-квадрат для непрерывных рас­преде­лений // Теория ве­ро­ятностей и ее применение. 1971. Т. XVI. № 1. – С. 3-20.

4.    Лемешко Б.Ю., Постовалов С.Н. О зависимости предельных распреде­ле­ний ста­тистик  Пирсона и отношения правдоподобия от способа группи­рования данных // Заводская лаборатория. 1998. Т. 64. – № 5. – С.56-63.

5.    Денисов В.И., Лемешко Б.Ю., Цой Е.Б. Оптимальное груп­пи­рование, оценка параметров и планирование регрессионных экспериментов: В 2 ч. / Новосиб. гос. техн. ун-т. - Новосибирск, 1993. – 346 с.

6.    Лемешко Б.Ю. Асимптотически оптимальное группирование наблю­де­ний - это обеспечение максимальной мощности критериев // Надеж­ность и контроль качества. – 1997. – № 8. – С. 3-14.

7.    Лемешко Б.Ю. Асимптотически оптимальное группирование наблю­де­ний в критериях согласия // Заводская лаборатория, 1998. Т. 64. – №1. – С.56-64.

8.    Денисов В.И., Лемешко Б.Ю., Постовалов С.Н. Прикладная статис­тика. Правила проверки согласия опытного распределения с тео­ретическим. Мето­­дические реко­мен­дации. Часть I. Критерии типа  . – Новоси­бирск: Изд-во НГТУ, 1998. – С. 126.

9.    Никулин М.С. Критерий хи-квадрат для непрерывных распределений с параметрами сдвига и масштаба // Теория вероятностей и ее приме­нение. 1973. Т. XVIII. № 3. – С.583-591.

10.Никулин М.С. О критерии хи-квадрат для непрерывных распре­де­лений // Теория вероятностей и ее применение. 1973. Т. XVIII. № 3. – С.675-676.

11.Мирвалиев М., Никулин М.С. Критерии согласия типа хи-квадрат // За­водская лаборатория. 1992. Т. 58. № 3. – С.52-58.

12.Aguirre N., Nikulin M. Chi-squared goodness-of-fit test for the family of logistic distributions // Kybernetika. 1994. V. 30. № 3. – P.214-222.

13.Лемешко Б.Ю., Постовалов С.Н. О распределениях статистик непара­мет­рических критериев согласия при оценивании по выборкам пара­метров на­блюдаемых законов // Заводская лаборатория. 1998. Т. 64. – № 3. – С. 61-72.

14.Орлов А.И. Методы оценки близости допредельных и предельных распределений статистик // Заводская лаборатория. 1998. Т. 64. – № 5. – С. 64-67.

15.Лемешко Б.Ю. Статистический анализ одномерных наблюдений слу­чай­ных величин: Программная система. – Новоси­бирск: Изд-во НГТУ. – 1995. – 125 с.

16.Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука, 1983. – 416 с.

17.Чибисов Д.М., Гванцеладзе Л.Г. О критериях согласия, основанных на группированных данных // III советско-японский симпозиум по теории вероятностей. Ташкент: изд-во “Фан”, 1975. – С. 183-185.

18.Боровков А.А. О мощности критерия  при увеличении числа групп // Теория вероятностей и ее применение. 1977. Т. XXII. № 2. – С.375-378.

 

 

[Содержание]