См. также: Прикладная математическая статистика (материалы к семинарам)

Заводская лаборатория. Диагностика материалов. 2003. Т. 69. – С..61–67.

УДК 519.2

О ВЫБОРЕ ЧИСЛА ИНТЕРВАЛОВ В КРИТЕРИЯХ СОГЛАСИЯ ТИПА [1]

Лемешко Б.Ю., Чимитова Е.В.

            Статистические свойства критериев типа  зависят как от того, каким образом область определения случайной величины разбивается на интервалы, так и от выбора числа интервалов группирования.

            Рекомендуемое в различных источниках количество интервалов группирования, используемое при вычислении оценок параметров, построении гистограмм, а также при проверке статистических гипотез с помощью критерия  Пирсона, колеблется в очень широких пределах. Большинство из рекомендуемых формул для оценки числа интервалов  носит эмпирический характер и обычно дает завышенные величины. Практически все рекомендации по выбору числа интервалов исходят из того, чтобы при данном объеме выборки  как можно лучше приблизить плотность распределения ее непараметрической оценкой (гистограммой). В данной работе выбор числа интервалов рассматривается с позиций построения наиболее мощного критерия согласия при близких конкурирующих гипотезах.

Естественно, что определение количества интервалов связывается с объемом выборки. В [1] на основании различных источников приводится целый ряд рекомендаций по выбору числа интервалов .

При выборе интервалов равной длины определяющим является требование, чтобы количество наблюдений, попавших в интервалы, было не слишком малым и сравнимым. При этом наиболее часто рекомендуется, чтобы количество наблюдений, попавших в интервал, было не менее 10. В [2] отмечается, что на практике допустимо, чтобы количество наблюдений в крайних интервалах было менее 5. В работах [3,4], в которых изучалась мощность критерия  Пирсона, говорится, что в случае унимодального распределения допускается уменьшение ожидаемых частот попадания наблюдений для одного или двух интервалов до 1 и даже ниже.

            Во многих источниках можно найти упоминание эвристической формулы Старджесса для определения “оптимального” числа интервалов [5]

.

            В [6] для определения “оптимального” числа интервалов рекомендуется формула Брукса и Каррузера

.

            В [7] рекомендуют соотношение

.

            В [4] для равновероятных интервалов их количество устанавливается порядка

,

где  - квантиль стандартного нормального распределения для заданного уровня значимости. В ряде работ приводятся модификации данной формулы. В [8] предлагается значение

,

а в [9] дальнейшее развитие этого соотношения

.

            В исследовании [10] получено соотношение

,

где  - значение контрэксцесса ().

            При больших объемах выборок  разброс значений , задаваемых различными формулами, достаточно велик. Поэтому на практике при выборе числа интервалов больше руководствуются разумными соображениями, выбирая число интервалов так, чтобы в интервалы попадало число наблюдений не менее 5-10. Так, например, в рекомендациях ВНИИМетрологии [11] в зависимости от  предлагаются следующие величины :

40–100	7–9
100–500	8–12
500–1000	10–16
1000–10000	12–22

            В [12] показано, что величина уклонения гистограммы от плотности распределения в лучшем случае имеет порядок , который достигается при числе интервалов  порядка . Но этот вывод сделан с позиций близости непрерывной функции плотности и гистограммы, а совсем не с позиций мощности критерия  Пирсона.

            В данном случае мы постараемся посмотреть, как отражается на мощности критериев типа  выбираемое число интервалов группирования .

            При справедливости простой проверяемой гипотезы  предельным распределением  стандартной статистики критерия согласия Пирсона , где  - объем выборки,  - количество наблюдений, попавших в -й интервал, 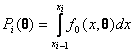 - вероятность попадания наблюдения в интервал,  - известный вектор параметров закона с плотностью , относительно которого проверяется гипотеза, - граничные точки интервалов, является -распределение. При проверке сложных гипотез и оценивании по этой же выборке в результате минимизации этой же статистики  компонент вектора параметров закона статистика  подчиняется -распределению. Статистика  подчиняется -распределению и в том случае, если используются оценки максимального правдоподобия по группированным наблюдениям (см. стр. 563-567 в [13], стр. 460-470 в [14] и [15]). Наши исследования методами статистического моделирования распределений данной статистики при проверке сложных гипотез и использовании оценок максимального правдоподобия по группированным наблюдениям (при конечных объемах выборок) также показали хорошее согласие получаемых эмпирических распределений статистики с -распределениями. При справедливой альтернативной гипотезе , соответствующей гипотетическому распределению с плотностью , предельное распределение  представляет собой нецентральное -распределение с тем же числом степеней свободы  или  и параметром нецентральности

,                                                                   (1)

где 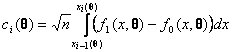. При использовании в процессе проверки сложных гипотез оценок максимального правдоподобия (ОМП) по исходным негруппированным наблюдениям распределения  и  отличаются от соответствующих -распределений. В частности, близость  к -распределению зависит от принятого способа разбиения выборки на интервалы [16].

            То, каким образом выбраны интервалы группирования, в основном отражается и отражается существенно на распределении . В [17-20] показано, что при фиксированном числе интервалов  и близких конкурирующих гипотезах  и  мощность критерия  Пирсона тем выше, чем меньше потери в информации Фишера, связанные с группированием наблюдений. Там же приводятся построенные таблицы, с инвариантными относительно параметров наблюдаемых законов асимптотически оптимальными границами интервалов для различных законов случайных величин.

В [21] и последующих работах [22-24] Никулиным предложено такое видоизменение стандартной статистики , при котором предельное распределение есть обычное распределение  (количество степеней свободы не зависит от числа оцениваемых параметров). Неизвестные параметры распределения  в этом случае должны оцениваться методом максимального правдоподобия по негруппированным данным. При этом вектор вероятностей попадания в интервалы  предполагается заданным, и граничные точки интервалов определяются соотношениями , . Предложенная статистика  отличается от  только при сложных гипотезах. Элементы и размерность матрицы 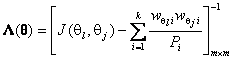 определяются оцениваемыми компонентами вектора параметров ,  - элементы информационной матрицы Фишера ,  - элементы вектора , величины  определяются соотношением . При верной альтернативе предельное распределение  представляет собой нецентральное -распределение с параметром нецентральности

,                                             (2)

где  - элементы вектора .

            Проведенные в [25] методами статистического моделирования исследования распределений статистики Никулина показали, что как , так и  слабо зависят от выбранного способа группирования и хорошо согласуются с соответствующими -распределениями. При этом критерий со статистикой Никулина при фиксированном числе интервалов  и фиксированном варианте группирования всегда мощнее критерия  Пирсона. Там же было отмечено, что если при разбиении области определения случайной величины на интервалы равной вероятности при близких конкурирующих гипотезах  и  с ростом  мощность критерия  Пирсона падает, то для критерия со статистикой Никулина при заданном объеме выборки  может существовать оптимальная величина числа интервалов , при котором критерий будет иметь максимальную мощность. Этот вывод относительно критерия  Пирсона хорошо согласуется с результатами работ [26-27].

В данной работе мы более подробно исследовали зависимость мощности от величины . Зная предельные распределения  и  статистики , для любого заданного уровня значимости  можно оценить мощность соответствующего критерия, рассматривая её как функцию от числа интервалов  при заданном объеме выборки . Исследование мощности критериев Пирсона и Никулина как функции  и  проводилось как аналитически, так и методами статистического моделирования. Причем приводимые результаты аналитических вычислений полностью подтверждаются оценками мощности, полученными на основании моделирования.

Мощность критериев типа  является функцией параметра нецентральности , задаваемого выражениями (1) или (2) соответственно. В свою очередь, параметр нецентральности  зависит от пары конкурирующих гипотез, числа интервалов , способа группирования и объема выборки .  При заданных вероятности ошибки первого рода  и числе степеней свободы  ( или ) величина мощности вычисляется в соответствии с выражением (см. стр. 63 в [28])

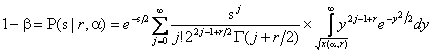,                (3)

где  есть -процентная точка -распределения с  степенями свободы,  - вероятность ошибки второго рода. Все приводимые ниже функции мощности строились при уровне значимости .

            На рис. 1 в зависимости от числа  равновероятных интервалов при различных  представлены функции мощности критерия  Пирсона при проверке простой гипотезы о согласии с экспоненциальным законом (: при ; :  при ). На рис. 2 приведены аналогичные функции при использовании асимптотически оптимального группирования [17,20]. Асимптотически оптимальные граничные точки, минимизирующие потери в информации Фишера, представлены в табл. 1. И в том и в другом случае с ростом  мощность падает, но в случае асимптотически оптимального группирования она выше, чем при равновероятном.

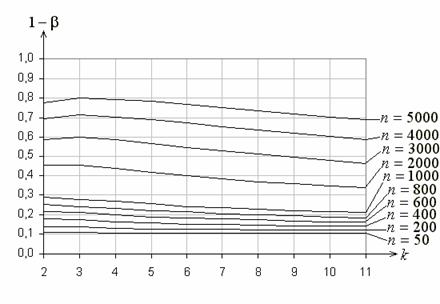
Рис. 1. Функции мощности критерия  Пирсона при проверке простой гипотезы

о согласии с экспоненциальным законом при равновероятном группировании

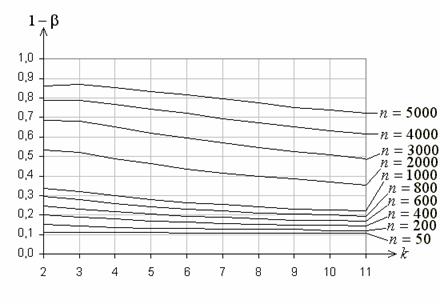
Рис. 2. Функции мощности критерия  Пирсона при проверке простой гипотезы

о согласии с экспоненциальным законом при асимптотически оптимальном группировании

Таблица 1

Оптимальные граничные точки интервалов группирования в виде  при проверке простых и сложных гипотез о согласии с экспоненциальным распределением по критериям типа и соответствующие значения относительной асимптотической информации

2	1.5936										0.6476
3	1.0176	2.6112									0.8203
4	0.7541	1.7716	3.3652								0.8910
5	0.6004	1.3545	2.3720	3.9657							0.9269
6	0.4993	1.0997	1.8538	2.8714	4.4650						0.9606
7	0.4276	0.9269	1.5273	2.2813	3.2989	4.8925					0.9606
8	0.3739	0.8015	1.3008	1.9012	2.6553	3.6729	5.2665				0.9693
9	0.3323	0.7063	1.1338	1.6331	2.2336	2.9876	4.0052	5.5988			0.9754
10	0.2990	0.6314	1.0053	1.4329	1.9322	2.5326	3.2866	4.3042	5.8979		0.9798
11	0.2716	0.5695	0.9014	1.2746	1.7015	2.1989	2.7955	3.5429	4.5480	6.1176	0.9832

Таблица 2

Оптимальные граничные точки интервалов группирования в виде  при проверке простых и сложных (при одновременном оценивании двух параметров) гипотез о согласии с нормальным распределением по критериям типа и соответствующие значения относительной асимптотической информации

3	-1.1106	1.1106													0.4065
4	-1.3834	0.0	1.3834												0.5527
5	-1.6961	-0.6894	0.6894	1.6961											0.6826
6	-1.8817	-0.9970	0.0	0.9970	1.8817										0.7557
7	-2.0600	-1.2647	-0.4918	0.4918	1.2647	2.0600									0.8103
8	-2.1954	-1.4552	-0.7863	0.0	0.7863	1.4552	2.1954								0.8474
9	-2.3188	-1.6218	-1.0223	-0.3828	0.3828	1.0223	1.6218	2.3188							0.8753
10	-2.4225	-1.7578	-1.2046	-0.6497	0.0	0.6497	1.2046	1.7578	2.4225						0.8960
11	-2.5167	-1.8784	-1.3602	-0.8621	-0.3143	0.3143	0.8621	1.3602	1.8784	2.5167					0.9121
12	-2.5993	-1.9028	-1.4914	-1.0331	-0.5334	0.0	0.5334	1.0331	1.4914	1.9028	2.5993				0.9247
13	-2.6746	-2.0762	-1.6068	-1.1784	-0.7465	-0.2669	0.2669	0.7465	1.1784	1.6068	2.0762	2.6746			0.9348
14	-2.7436	-2.1609	-1.7092	-1.3042	-0.9065	-0.4818	0.0	0.4818	0.9065	1.3042	1.7092	2.1609	2.7436		0.9430
15	-2.8069	-2.2378	-1.8011	-1.4150	-1.0435	-0.6590	-0.2325	0.2325	0.6590	1.0435	1.4150	1.8011	2.2378	2.8069	0.9498

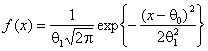На рис. 3 приведены функции мощности критерия  Пирсона в случае разбиения области определения случайной величины на интервалы равной вероятности при проверке простой гипотезы о согласии с нормальным законом :  при ,  против : нормальный закон при , . На рис. 4 аналогичные функции мощности в случае использования асимптотически оптимального группирования [15,18]. Асимптотически оптимальные граничные точки, минимизирующие потери в информации Фишера, представлены в табл. 2.

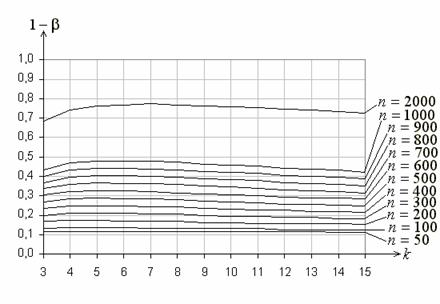
Рис. 3. Функции мощности критерия  Пирсона при проверке простой гипотезы

о согласии с нормальным законом при равновероятном группировании

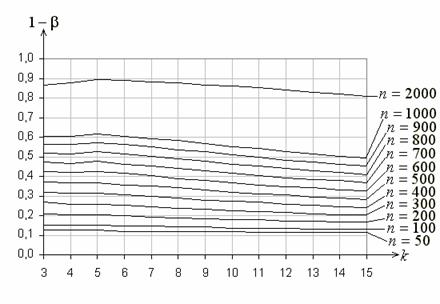
Рис. 4. Функции мощности критерия  Пирсона при проверке простой гипотезы

о согласии с нормальным законом при асимптотически оптимальном группировании

На рис. 5-8 представлены функции мощности критерия  Пирсона при проверке простых и сложных гипотез о согласии с нормальным законом : 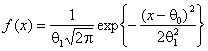, когда в качестве альтернативы рассматривается логистический закон : 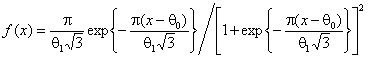при значениях параметров , . На рис. 5 представлены функции мощности для случая равновероятного группирования и проверки простой гипотезы, соответствующей нормальному закону с параметрами , . На рис. 6 то же, но при проверке сложной гипотезы. Как видим, и здесь с ростом  мощность падает. При проверке простой гипотезы функция мощности критерия Пирсона для  принимает максимальное значение при , и при дальнейшем увеличении объема выборки это оптимальное число интервалов не изменяется.

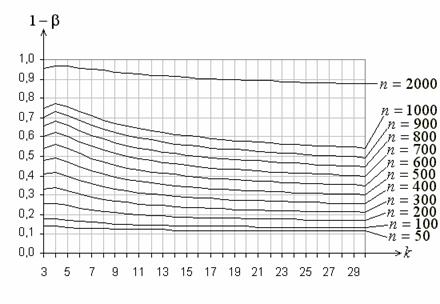
Рис. 5. Функции мощности критерия  Пирсона при проверке простой гипотезы

о согласии с нормальным законом при равновероятном группировании

и альтернативе, соответствующей логистическому закону

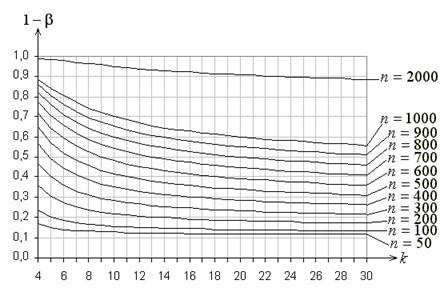
Рис. 6. Функции мощности критерия  Пирсона при проверке сложной гипотезы

 о согласии с нормальным законом при равновероятном группировании

и альтернативе, соответствующей логистическому закону

            В случае проверки сложной гипотезы и оценивании по выборке параметров гипотетического распределения функция мощности критерия Пирсона принимает наибольшее значение при минимально возможном числе интервалов  и далее монотонно убывает с ростом  (рис. 6).

            На рис. 7 отражены функции мощности критерия  Пирсона для вышеприведенной пары альтернатив при проверке простой гипотезы, а на рис. 8 при проверке сложной в случае применения асимптотически оптимального группирования. Здесь функции мощности представляют собой более интересную картину с провалами при  и . Эти провалы свидетельствуют о том, что при таких комбинациях граничных точек, не смотря на минимальные потери в информации Фишера, две рассматриваемые конкурирующие гипотезы плохо различаются. При дальнейшем росте  происходит увеличение мощности критерия.

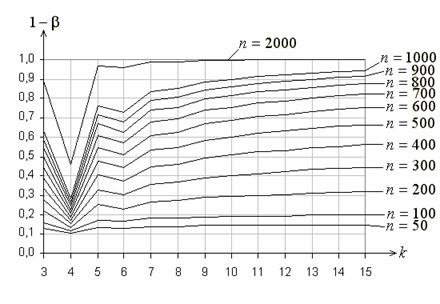
Рис. 7. Функции мощности критерия  Пирсона при проверке простой гипотезы

о согласии с нормальным законом при асимптотически оптимальном группировании

и альтернативе, соответствующей логистическому закону

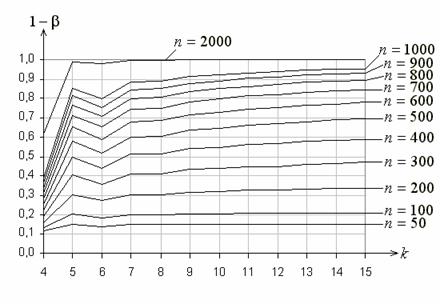
Рис. 8. Функции мощности критерия  Пирсона при проверке сложной гипотезы

 о согласии с нормальным законом при асимптотически оптимальном группировании

и альтернативе, соответствующей логистическому закону

            Функция мощности критерия типа  Никулина, как следует из рис. 9, на области значений , содержащей максимальное значение мощности, является выпуклой вверх функцией.

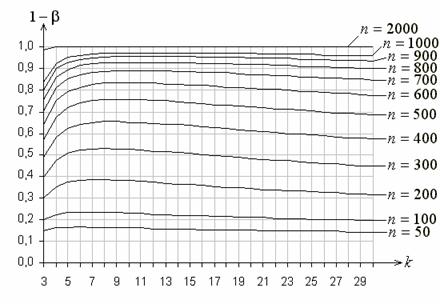
Рис. 9. Функции мощности критерия типа  Никулина при проверке

сложной гипотезы о согласии с нормальным законом при равновероятном

группировании и альтернативе, соответствующей логистическому закону

            Отметим, что статистическое моделирование распределений статистик, которое проводилось нами в целях контроля результатов, полностью подтверждает аналитические расчеты, проиллюстрированные на приводимых рисунках.

Выводы   

            При проверке согласия опытного распределения с теоретической моделью нас в первую очередь должна интересовать возможность с помощью критерия уловить отклонения в наблюдаемых данных, которые говорят о предпочтительности некоторой другой достаточно близкой к проверяемой модели, то есть возможность различать близкие гипотезы. Это означает, что мы должны использовать критерии, которые обладают наибольшей мощностью против близких альтернатив.

            Максимизировать мощность критериев  Пирсона и отношения правдоподобия [13] можно за счет двух факторов: выбирая в качестве способа разбиения на интервалы асимптотически оптимальное группирование [17-20] и подбирая “оптимальное” число интервалов .

            Мощность критерия Никулина можно максимизировать только за счет выбора “оптимального” числа интервалов, так как наиболее предпочтительным способом группирования, по-видимому, является разбиение на интервалы равной вероятности [25].

            Найти “оптимальное” число интервалов  для соответствующего критерия можно, максимизировав по  соотношение (3). При этом фиксируется пара конкурирующих гипотез, способ группирования, объем выборки  и вероятность ошибки первого рода .

            Мощность критериев  Пирсона и отношения правдоподобия часто оказывается максимальной против близких конкурирующих гипотез, если выборку разбивать на минимально возможное число интервалов группирования. С ростом же числа интервалов мощность критериев падает. Этот факт ускользает от внимания большинства исследователей, использующих данный критерий, и совсем не упоминается в рекомендациях различного уровня.

            В некоторых ситуациях, то есть при конкретных парах конкурирующих гипотез, функции мощности критериев  Пирсона и отношения правдоподобия оказываются выпуклыми вверх по , и существует “оптимальное” значение числа интервалов. Однако это “оптимальное” значение обычно достаточно мало отличается от минимально возможного и незначительно изменяется в сторону увеличения при значительном росте объема выборки . Прослеживается зависимость “оптимальной” величины  не только от объёма выборки, пары конкурирующих гипотез, но и от способа группирования.

            Функция мощности критерия Никулина обычно оказывается выпуклой вверх по . Поэтому “оптимальное” число интервалов обычно существует. Это “оптимальное” значение растет с увеличением объема выборки. Но его величина также меньше значений, рекомендуемых любыми действующими регламентирующими документами и справочными источниками.

            И еще одно замечание. В последние годы в сознании многих исследователей сформировалось устоявшееся мнение о критериях типа  как о плохих критериях согласия. В этой связи естественным оказывается вопрос, зачем использовать критерии типа , если есть критерии Колмогорова и Мизеса? Имеется, как минимум, две причины обосновывающие рекомендации применения критериев типа . Во-первых, с позиций наибольшей мощности против близких альтернатив в случае проверки простых гипотез и использовании в критериях типа  асимптотически оптимального группирования критерии типа  оказываются предпочтительнее критериев Колмогорова и Мизеса [25]. При проверке простых гипотез наблюдается следующий порядок предпочтения (по мощности):

типа  Колмогорова Мизеса.

При проверке сложных гипотез порядок предпочтения меняется:

типа Мизеса  типа Колмогорова  Никулина  Пирсона.

Однако отсюда и вытекает вторая причина: критерии типа Колмогорова и типа Мизеса при проверке сложных гипотез теряют “свободу от распределения”. В то время как для критериев Никулина и  Пирсона предельные распределения статистик при проверке сложных гипотез известны. Конечно, для некоторых частных случаев различными способами получены модели предельных распределений статистик критериев типа Колмогорова, типа  и Мизеса. Наиболее широко, по-видимому, они представлены в [29,30]. Однако это далеко не снимает остроту проблемы. Есть и третий довод. Критерии согласия используют различные меры близости распределений, по-разному улавливают различные отклонения в наблюдаемых данных от предполагаемых законов распределений. Поэтому не следует обеднять методику статистического анализа, отказываясь от какого-либо из зарекомендовавших себя критериев. Лучше всего использовать их совокупность.

ЛИТЕРАТУРА

1. Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. - Л.: Энергоатомиздат, 1991. - 303 с.

2. Cochran W.G. Some Methods of Strengthening the Common  Tests // Biometrics, 1954. V. 10. - P. 417.

3. Mann H.B., Wald A. On the choice of the number of intervals in the application of the chi-square test // Ann. Math. Stat., 1942. V. 13. - P. 478-479.

4. Mann H.B., Wald A. On the choice of the number of class intervals in the application of the chi square test // Ann. Math. Stat., 1942. V. 13. - P. 306-317.

5. Sturgess H.A. The choice of classic intervals // J. Am. Statist. Assoc. - march 1926. - 47 p.

6. Шторм Р. Теория вероятностей. Математическая статистика. Статистический контроль качества. - М.: Мир, 1970. - 368 с.

7. Heinhold I., Gaede K.W. Ingeniur statistic. - München; Wien, Springler Verlag, 1964. - 352 s.

8. Таушанов З., Тонева Е., Пенова Р. Вычисление энтропийного коэффициента при малых выборках // Изобретательство, стандартизация и качество, 1973. № 5. - София.

9. Тонева Е. Аппроксимация распределений погрешности средств измерений // Измерительная техника, 1981. № 6. - С. 15-16.

10. Алексеева И.У. Теоретическое и экспериментальное исследование законов распределения погрешностей, их классификация и методы оценки их параметров: Автореф. дис. на соиск. учен. степени кан. техн. наук. - Л., 1975. - 20 с.

11. Бурдун Г.Д., Марков Б.Н. Основы метрологии. - М.: Изд-во стандартов, 1985. - 120 с.

12. Ченцов Н.Н. Статистические решающие правила и оптимальные выводы. - М.: Наука, 1972. - 520 с.

13. Кендалл М., Стьюарт А. Статистические выводы и связи. - М.: Наука, 1973. - 900 с.

14. Крамер Г. Математические методы статистики. - М.: Мир, 1975. - 648 с.

15. Birch M.W. A new proof of the Pearson–Fisher theorem // Ann. Math. Statist. – 1964. V. 35. – P. 817.

16. Лемешко Б.Ю., Постовалов С.Н. О зависимости предельных распределений статистик  Пирсона и отношения правдоподобия от способа группирования данных // Заводская лаборатория. 1998. Т. 64. – № 5. – С.56-63.

17. Денисов В.И., Лемешко Б.Ю., Цой Е.Б. Оптимальное группирование, оценка параметров и планирование регрессионных экспериментов: В 2 ч. / Новосиб. гос. техн. ун-т. - Новосибирск, 1993. – 346 с.

18. Лемешко Б.Ю. Асимптотически оптимальное группирование наблюдений - это обеспечение максимальной мощности критериев // Надежность и контроль качества. – 1997. – № 8. – С. 3-14.

19. Лемешко Б.Ю. Асимптотически оптимальное группирование наблюдений в критериях согласия // Заводская лаборатория, 1998. Т. 64. – №1. – С.56-64.

20. Денисов В.И., Лемешко Б.Ю., Постовалов С.Н. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Методические рекомендации. Часть I. Критерии типа  . – Новосибирск: Изд-во НГТУ, 1998. – С. 126.

21. Никулин М.С. О критерии хи-квадрат для непрерывных распределений // Теория вероятностей и её применение. 1973. Т.XVIII. – № 3. – С.675-676.

22. Никулин М.С. Критерий хи-квадрат для непрерывных распределений с параметрами сдвига и масштаба // Теория вероятностей и ее применение. 1973. Т. XVIII. – № 3. – С.583-591.

23. Мирвалиев М., Никулин М.С. Критерии согласия типа хи-квадрат // Заводская лаборатория. 1992. Т. 58. – № 3. – С.52-58.

24. Aguirre N., Nikulin M. Chi-squared goodness-of-fit test for the family of logistic distributions // Kybernetika. 1994. V. 30. – № 3. – P.214-222.

25. Лемешко Б.Ю., Постовалов С.Н., Чимитова Е.В. О распределениях статистики и мощности критерия типа  Никулина // “Заводская лаборатория. Диагностика материалов”, 2001. Т. 67. – №5. (в печати).

26. Чибисов Д.М., Гванцеладзе Л.Г. О критериях согласия, основанных на группированных данных // III советско-японский симпозиум по теории вероятностей. Ташкент: изд-во “Фан”, 1975. – С. 183-185.

27. Боровков А.А. О мощности критерия  при увеличении числа групп // Теория вероятностей и ее применение. 1977. Т. XXII. – № 2. – С.375-378.

28. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. - М.: Наука, 1983. - 416 с.

29. Лемешко Б.Ю., Постовалов С.Н. О распределениях статистик непараметрических критериев согласия при оценивании по выборкам параметров наблюдаемых законов // Заводская лаборатория. 1998. – № 3. – С. 61-72.

30. Лемешко Б.Ю., Постовалов С.Н. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Методические рекомендации. Часть II. Непараметрические критерии. – Новосибирск: Изд-во НГТУ, 1999. –  85 c.

Таблица 3

Теоретические значения мощности критерия  Пирсона в случае проверки простой гипотезы о согласии с нормальным законом  при равновероятном группировании и альтернативе, соответствующей логистическому закону

k	n=50	n=100	n=200	n=300	n=400	n=500	n=600	n=700	n=800	n=900	n=1000	n=2000
3	0,1389	0,1784	0,2577	0,3353	0,4095	0,4793	0,5438	0,6026	0,6558	0,7033	0,7455	0,9548
4	0,1384	0,1781	0,2595	0,3409	0,4196	0,4939	0,5625	0,6248	0,6806	0,7299	0,7730	0,9693
5	0,1346	0,1709	0,2465	0,3236	0,3995	0,4723	0,5405	0,6032	0,6601	0,7109	0,7557	0,9659
6	0,1313	0,1643	0,2339	0,3059	0,3779	0,4480	0,5146	0,5768	0,6339	0,6856	0,7319	0,9593
7	0,1286	0,1590	0,2235	0,2911	0,3595	0,4268	0,4916	0,5528	0,6097	0,6618	0,7090	0,9519
8	0,1266	0,1549	0,2153	0,2791	0,3443	0,4092	0,4722	0,5324	0,5888	0,6411	0,6888	0,9446
9	0,1250	0,1516	0,2088	0,2695	0,3320	0,3947	0,4561	0,5152	0,5712	0,6233	0,6714	0,9379
10	0,1237	0,1490	0,2035	0,2617	0,3219	0,3827	0,4427	0,5009	0,5562	0,6083	0,6565	0,9318
11	0,1227	0,1469	0,1991	0,2552	0,3135	0,3727	0,4315	0,4887	0,5435	0,5954	0,6437	0,9262
12	0,1218	0,1451	0,1955	0,2498	0,3065	0,3642	0,4219	0,4783	0,5326	0,5842	0,6326	0,9213
13	0,1211	0,1436	0,1924	0,2451	0,3004	0,3570	0,4136	0,4693	0,5232	0,5745	0,6229	0,9168
14	0,1204	0,1423	0,1898	0,2411	0,2952	0,3507	0,4064	0,4615	0,5149	0,5660	0,6143	0,9128
15	0,1199	0,1412	0,1874	0,2377	0,2906	0,3452	0,4001	0,4546	0,5076	0,5585	0,6067	0,9091
16	0,1194	0,1402	0,1854	0,2346	0,2866	0,3403	0,3945	0,4484	0,5010	0,5517	0,5999	0,9058
17	0,1190	0,1393	0,1836	0,2319	0,2830	0,3359	0,3895	0,4429	0,4951	0,5456	0,5937	0,9027
18	0,1186	0,1386	0,1820	0,2294	0,2797	0,3319	0,3849	0,4378	0,4898	0,5401	0,5881	0,8998
19	0,1183	0,1379	0,1806	0,2272	0,2768	0,3283	0,3808	0,4333	0,4849	0,5350	0,5830	0,8972
20	0,1180	0,1372	0,1792	0,2252	0,2741	0,3251	0,3770	0,4291	0,4804	0,5303	0,5782	0,8947
21	0,1177	0,1366	0,1780	0,2233	0,2717	0,3220	0,3735	0,4252	0,4763	0,5260	0,5738	0,8924
22	0,1174	0,1361	0,1769	0,2216	0,2694	0,3192	0,3703	0,4216	0,4724	0,5219	0,5696	0,8902
23	0,1172	0,1356	0,1759	0,2200	0,2673	0,3166	0,3673	0,4182	0,4688	0,5182	0,5658	0,8881
24	0,1170	0,1352	0,1749	0,2186	0,2653	0,3142	0,3644	0,4151	0,4654	0,5146	0,5621	0,8861
25	0,1168	0,1347	0,1740	0,2172	0,2634	0,3119	0,3618	0,4121	0,4622	0,5112	0,5587	0,8842
26	0,1166	0,1343	0,1732	0,2159	0,2617	0,3098	0,3593	0,4093	0,4591	0,5080	0,5554	0,8824
27	0,1164	0,1339	0,1724	0,2147	0,2601	0,3077	0,3569	0,4066	0,4563	0,5050	0,5523	0,8806
28	0,1162	0,1336	0,1716	0,2135	0,2585	0,3058	0,3546	0,4041	0,4535	0,5021	0,5493	0,8789
29	0,1160	0,1333	0,1709	0,2124	0,2570	0,3040	0,3525	0,4017	0,4509	0,4993	0,5465	0,8772
30	0,1159	0,1329	0,1703	0,2114	0,2556	0,3023	0,3504	0,3994	0,4484	0,4967	0,5437	0,8756

Таблица 4

Теоретические значения мощности критерия  Пирсона в случае проверки сложной гипотезы о согласии с нормальным законом при равновероятном группировании и альтернативе, соответствующей логистическому закону

k	n=50	n=100	n=200	n=300	n=400	n=500	n=600	n=700	n=800	n=900	n=1000	n=2000
4	0,1688	0,2355	0,3600	0,4708	0,5669	0,6488	0,7175	0,7744	0,8209	0,8587	0,8890	0,9920
5	0,1507	0,2021	0,3043	0,4019	0,4921	0,5734	0,6451	0,7072	0,7604	0,8053	0,8427	0,9858
6	0,1416	0,1847	0,2730	0,3607	0,4446	0,5228	0,5941	0,6577	0,7138	0,7624	0,8041	0,9787
7	0,1360	0,1737	0,2524	0,3324	0,4109	0,4857	0,5554	0,6190	0,6762	0,7269	0,7713	0,9712
8	0,1322	0,1661	0,2378	0,3119	0,3858	0,4574	0,5252	0,5882	0,6458	0,6976	0,7436	0,9637
9	0,1294	0,1606	0,2270	0,2964	0,3665	0,4353	0,5013	0,5634	0,6209	0,6732	0,7204	0,9567
10	0,1273	0,1564	0,2186	0,2843	0,3513	0,4177	0,4820	0,5431	0,6003	0,6529	0,7007	0,9501
11	0,1257	0,1531	0,2120	0,2747	0,3390	0,4033	0,4661	0,5263	0,5830	0,6357	0,6839	0,9441
12	0,1244	0,1505	0,2067	0,2668	0,3289	0,3913	0,4528	0,5121	0,5684	0,6210	0,6695	0,9386
13	0,1233	0,1483	0,2023	0,2602	0,3204	0,3813	0,4415	0,5000	0,5558	0,6083	0,6570	0,9336
14	0,1225	0,1465	0,1986	0,2546	0,3132	0,3727	0,4318	0,4896	0,5449	0,5972	0,6460	0,9291
15	0,1217	0,1449	0,1954	0,2499	0,3069	0,3652	0,4234	0,4804	0,5353	0,5875	0,6363	0,9249
16	0,1210	0,1436	0,1926	0,2457	0,3015	0,3587	0,4160	0,4724	0,5269	0,5788	0,6276	0,9210
17	0,1205	0,1424	0,1902	0,2421	0,2967	0,3529	0,4094	0,4652	0,5193	0,5710	0,6198	0,9175
18	0,1200	0,1414	0,1880	0,2388	0,2925	0,3477	0,4035	0,4587	0,5124	0,5639	0,6127	0,9142
19	0,1195	0,1405	0,1861	0,2359	0,2886	0,3431	0,3982	0,4528	0,5062	0,5575	0,6062	0,9111
20	0,1191	0,1396	0,1844	0,2333	0,2852	0,3389	0,3933	0,4475	0,5005	0,5517	0,6003	0,9083
21	0,1188	0,1389	0,1829	0,2309	0,2820	0,3350	0,3889	0,4426	0,4953	0,5462	0,5948	0,9056
22	0,1184	0,1382	0,1814	0,2287	0,2791	0,3315	0,3848	0,4381	0,4905	0,5412	0,5897	0,9030
23	0,1181	0,1376	0,1801	0,2267	0,2764	0,3282	0,3810	0,4339	0,4860	0,5365	0,5850	0,9006
24	0,1178	0,1370	0,1789	0,2249	0,2740	0,3252	0,3775	0,4300	0,4818	0,5322	0,5805	0,8983
25	0,1176	0,1365	0,1778	0,2232	0,2717	0,3223	0,3742	0,4263	0,4779	0,5281	0,5763	0,8961
26	0,1173	0,1360	0,1768	0,2216	0,2695	0,3197	0,3711	0,4229	0,4742	0,5242	0,5723	0,8939
27	0,1171	0,1355	0,1758	0,2201	0,2675	0,3172	0,3682	0,4197	0,4707	0,5205	0,5686	0,8919
28	0,1169	0,1351	0,1749	0,2187	0,2656	0,3149	0,3655	0,4166	0,4673	0,5170	0,5650	0,8899
29	0,1167	0,1347	0,1740	0,2173	0,2638	0,3127	0,3629	0,4137	0,4642	0,5137	0,5616	0,8880
30	0,1165	0,1343	0,1732	0,2161	0,2621	0,3106	0,3604	0,4109	0,4612	0,5106	0,5584	0,8862

Таблица 5

Теоретические значения мощности критерия  Пирсона в случае проверки простой гипотезы о согласии с нормальным законом  при асимптотически оптимальном группировании и альтернативе, соответствующей логистическому закону

k	n=50	n=100	n=200	n=300	n=400	n=500	n=600	n=700	n=800	n=900	n=1000	n=2000
3	0,12916	0,15868	0,21819	0,27740	0,33541	0,39151	0,44520	0,49610	0,54397	0,58868	0,63016	0,88864
4	0,10858	0,11726	0,13486	0,15275	0,17088	0,18920	0,20767	0,22624	0,24486	0,26351	0,28215	0,46133
5	0,13512	0,17194	0,24874	0,32696	0,40386	0,47741	0,54618	0,60929	0,66629	0,71705	0,76172	0,96801
6	0,13081	0,16331	0,23185	0,30284	0,37390	0,44315	0,50915	0,57089	0,62774	0,67936	0,72565	0,95678
7	0,13873	0,18034	0,26907	0,36049	0,45003	0,53438	0,61137	0,67981	0,73932	0,79008	0,83266	0,98867
8	0,13919	0,18166	0,27297	0,36760	0,46037	0,54751	0,62657	0,69627	0,75623	0,80674	0,84850	0,99176
9	0,14210	0,18820	0,28803	0,39138	0,49167	0,58429	0,66647	0,73703	0,79594	0,84394	0,88225	0,99598
10	0,14307	0,19058	0,29411	0,40154	0,50549	0,60079	0,68448	0,75538	0,81366	0,86033	0,89685	0,99732
11	0,14443	0,19380	0,30198	0,41428	0,52234	0,62042	0,70536	0,77614	0,83320	0,87791	0,91210	0,99833
12	0,14495	0,19519	0,30581	0,42090	0,53143	0,63123	0,71700	0,78775	0,84411	0,88767	0,92048	0,99879
13	0,14591	0,19753	0,31168	0,43049	0,54407	0,64579	0,73221	0,80250	0,85760	0,89943	0,93030	0,99919
14	0,14645	0,19892	0,31545	0,43688	0,55267	0,65578	0,74268	0,81264	0,86681	0,90738	0,93687	0,99941
15	0,14692	0,20016	0,31882	0,44262	0,56039	0,66471	0,75197	0,82154	0,87481	0,91420	0,94243	0,99956

Таблица 6

Теоретические значения мощности критерия  Пирсона в случае проверки сложной гипотезы о согласии с нормальным законом  при асимптотически оптимальном группировании и альтернативе, соответствующей логистическому закону

k	n=50	n=100	n=200	n=300	n=400	n=500	n=600	n=700	n=800	n=900	n=1000	n=2000
4	0,11583	0,13157	0,16276	0,19351	0,22376	0,25344	0,28252	0,31095	0,33870	0,36575	0,39208	0,61395
5	0,15143	0,20361	0,30721	0,40603	0,49713	0,57894	0,65088	0,71306	0,76601	0,81056	0,84763	0,98679
6	0,14098	0,18345	0,27049	0,35701	0,44003	0,51754	0,58832	0,65178	0,70780	0,75659	0,79860	0,97715
7	0,14856	0,19996	0,30658	0,41205	0,51096	0,60007	0,67785	0,74399	0,79903	0,84397	0,88009	0,99431
8	0,14732	0,19805	0,30478	0,41168	0,51263	0,60382	0,68334	0,75072	0,80644	0,85157	0,88747	0,99558
9	0,14946	0,20318	0,31728	0,43169	0,53884	0,63416	0,71557	0,78284	0,83689	0,87929	0,91187	0,99782
10	0,14960	0,20397	0,32048	0,43796	0,54797	0,64540	0,72795	0,79542	0,84892	0,89024	0,92145	0,99850
11	0,15037	0,20607	0,32630	0,44783	0,56122	0,66080	0,74417	0,81127	0,86354	0,90310	0,93233	0,99905
12	0,15033	0,20637	0,32815	0,45178	0,56715	0,66816	0,75221	0,81932	0,87105	0,90975	0,93794	0,99929
13	0,15089	0,20793	0,33256	0,45933	0,57726	0,67979	0,76425	0,83082	0,88137	0,91855	0,94514	0,99952
14	0,15105	0,20859	0,33496	0,46385	0,58362	0,68731	0,77214	0,83841	0,88819	0,92434	0,94984	0,99964
15	0,15120	0,20918	0,33714	0,46797	0,58940	0,69410	0,77923	0,84516	0,89419	0,92937	0,95386	0,99973

---

[1] Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 00-01-00913)

[Содержание]