См. также: Прикладная математическая статистика (материалы к семинарам)

 

Заводская лаборатория. Диагностика материалов. 2003. Т. 69. – С.62-68.

 

УДК 519.2

 

ЧИСЛЕННОЕ СРАВНЕНИЕ ОЦЕНОК МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ С ОДНОШАГОВЫМИ И ВЛИЯНИЕ ТОЧНОСТИ ОЦЕНИВАНИЯ НА РАСПРЕДЕЛЕНИЯ СТАТИСТИК КРИТЕРИЕВ СОГЛАСИЯ[1]

 

Б.Ю. Лемешко, Е.В. Чимитова

Новосибирский государственный технический университет

E-mail: headrd@fpm.ami.nstu.ru

 

 

Предельные распределения  статистик  критериев согласия типа Колмогорова, Смирнова, типа  и  Мизеса при проверке сложных ги­потез вида :  существенно зависят от приме­ня­емого метода оценивания [1,2]. При проверке таких сложных гипотез оценка вектора параметров , принадлежащая пространству параметров , вычисля­ется по той же выборке, по которой оцениваются и параметры.

Зависимость условных распределений  от метода оце­нивания настолько значительна, что ни в коем случае нельзя при вычислении вероят­но­сти , где  – значение статистики найден­ное по вы­борке, применять распределение статистики, соот­вет­ствующее друго­му методу оценивания.

Насколько сильно отличаются распреде­ле­ния одних и тех же ста­тистик при использовании различных методов оце­ни­ва­ния – показано в работах [1,2]. В [2] приведены таблицы с построенными аппроксимациями предель­ных рас­пределений минимумов статистик крите­риев со­гла­­сия типа Колмо­горова, типа  и  Мизеса и распределений статистик при использовании метода максимального правдо­подобия, уточня­ющие результаты работы [3].

При вычислении оценок максимального правдоподобия (ОМП), как пра­вило, возникает необходимость численного решения уравнений правдо­подобия, что является достаточно сложной задачей. К тому же в некоторых случаях функция правдоподобия имеет много локальных максимумов, что дополни­тельно усложняет задачу [4] (авторам приходилось сталкиваться с многоэкс­тремальностью функции правдоподобия). Ещё Р. Фишером было предполо­жено, что во многих регулярных случаях для достижения хорошей аппрокси­мации будет достаточно осуществить только один итерационный цикл при ре­шении уравнений правдоподобия. Позднее были сформулированы и доказаны теоремы о том, что при определенных условиях регулярности, накладывае­мых на функцию плотности, асимптотические свойства ОМП и оценок, полу­ченных в результате первой итерации решения системы уравнений правдопо­добия методом Ньютона-Рафсона (одношаговых оценок или ОШ-оценок, на графиках и в формулах в дальнейшем использовано сокращение ОШО), совпадают [4-7].  Это означает, что асимптотическая дисперсия ОШ-оценок, как и асимп­тотическая дисперсия ОМП, определяется соотношением

,

где  – информа­ци­он­ная матрица Фишера.

Рассмотрим получение ОМП и ОШ-оценок. Пусть наблюдается выборка  независимых одинаково распределенных случайных величин  с плотностью распределения . Тре­буется оценить неизвестный параметр . ОМП вектора парамет­ров  вычисляется в результате максимизации функции правдоподобия

 или, что является более удобным, ее логарифма

.                                      (1)

Обычно  находят, решая систему уравнений правдоподобия

,  .                                        (2)

В тех случаях, когда ОМП нельзя получить в виде аналитических выра­жений, задачи (1) или (2) могут решаться численно с использованием какого-либо итерационного процесса.

В методах Ньютона-Рафсона и накопления Рао [8] очередное прибли­же­ние ОМП определяется соотношением

,                                    (3)

где вектор  – градиент логарифма функции правдоподобия с компо­нентами , . В методе Ньютона-Рафсона матрица  представляет собой матрицу вторых частных производных логарифма функ­ции правдоподобия с элементами

,  .

В методе накопления Рао матрица . Элементы информа­ци­он­ной матрицы Фишера  определяются выражением

,  ,

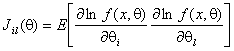где  – оператор математического ожидания.

ОШ-оценки определяются соотношением

.                                 (4)

При этом в качестве начального приближения  нельзя брать произвольное зна­чение. В качестве  может быть взята некоторая асимптотически нормаль­ная оценка и тогда  с точностью до  приближает  [6]. В [7] в качестве  рекомендуются состоятельные оценки, вычисляемые по методу моментов или по выборочным квантилям. Именно при выборе таких начальных приближений ОШ-оценки оказываются асимптотически эффективными.

В работе [7] ОШ-оценкам придается очень большое самостоятельное зна­чение. Они, в каком то смысле, даже противопоставляются ОМП. Авторы не склонны так преувеличивать роль ОШ-оценок, но согласны с их большим зна­чением для практики статистических вычислений.

Как уже сказано, условные распределения  статистик одних и тех же критериев согласия карди­нально отличаются при различных методах оценивания. Однако хотелось бы знать, как отразится на распределениях стати­стик использование приближенных оценок того же вида, имеющих такие же асимптотические свойства? Вопрос заключается в том, можем ли мы при про­верке сложных гипотез о согласии эмпирического распределения с теоретиче­ским и применении ОШ-оценок параметров использовать предельные распре­деления статистик , построенные в предположении вычисления “точ­ных” ОМП параметров наблюдаемого закона? В определенной степени по­ложительный ответ на этот вопрос очевиден: одинаковые асимптотические свойства оценок предопределяют совпадение предельных распределений стати­стик соответствующих критериев согласия. На практике же, осуществляя ста­тистические выводы, мы опираемся на выборки конечного размера. И совпаде­ние асимптотических свойств оценок не всегда говорит об одинаковых свойст­вах тех же оценок при конечных объемах выборок. И будут ли одина­ковыми распределения статистик критериев, построенные с использованием ОМП и ОШ-оценок по выборкам ограниченного объема? А что будет с распределе­ниями ОШ-оценок и, соответственно, с распределениями статистик критериев согласия, если начальные приближения  в силу разных причин окажутся не соответствующими условиям теорем в [7] или [6]?

Необходимость проведения такого исследования стала очевидной в про­цессе обсуждения с А.И. Орловым проблем точности построения моделей пре­дельных распределений статистик непараметрических критериев согласия с ис­пользованием методов статистического моделирования [9]. В результате во­з­никла идея, используя методы компьютерного моделирования, сравнить стати­стические свойства ОМП и ОШ-оценок при конечных объемах выборок и по­смотреть, как имеющиеся различия в свойствах оценок, если они значимы, от­ражаются на распреде­лениях статистик критериев.

Исследования проводились на примере двухпараметрических распре­де­лений Вейбулла (Вейбулла-Гнеденко) с функцией плотности 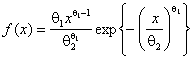 и гамма-распределения , где  – параметр формы,  – параметр масштаба, . В качестве начальных приближений  использовались оценки, вычисляемые по методу моментов (ОММ). В случае распределения Вейбулла ОММ вычисляются как корни системы уравнений

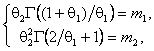
где  и - соответственно первый и второй выборочные моменты. В случае гамма-распределения [10] на основании соотношений

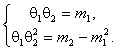
Исследовались распределения ОМП, ОШ-оценок, ОММ и эмпирические распределения статистик критерия согласия типа Колмогорова [11] и типа  Мизеса, полученные в случае применения соответствующих оценок. В иссле­дуемом критерии типа Колмогорова используется стати­стика вида [12]

,

где

 - объем выборки,  - упорядоченные по возрастанию вы­бо­роч­ные значения,  - функция закона распределения, согласие с которым про­ве­ряется, в критерии типа  Мизеса – статистика [12]

.

Исследование предельных распределений статистик непараметрических критериев согласия при проверке сложных гипотез с использованием ОШ-оце­нок, ОМП и ОММ проводилось с исполь­зованием методики компьютерного анализа статистических закономерностей. Эмпири­ческие функции распре­деле­ний оценок и распределений статистик строились по количеству моделируемых выборок . При этом оценки параметров и статистики вычислялись по выборкам псевдослучайных величин объемом . Выборки моделирова­лись в соответствии с распределением Вейбулла и гамма-распределением с па­раметрами , .

На приводимых ниже рисунках иллюстрируются некоторые из по­стро­ен­ных на основании резуль­татов моделирования эмпирические распределения оценок и распределения статистик критериев согласия типа Колмогорова или типа  Мизеса при проверке сложных гипотез и использовании соответ­ству­ющих оценок. На каждом из рисунков приведены плотности распределений оценок или эмпирические распределения статистик критериев согласия. Соот­ветствующие распределения помечены на рисунках и в тех случаях, когда визу­ально они совпадают.

Было проведено четыре цикла испытаний.

a) Исследовались распределения оценок и распределения статистик кри­териев согласия при одновременном оценивании двух параметров закона рас­пре­деления Вейбулла или гамма-распределения. В качестве начального прибли­жения  использовались оценки по методу моментов.

b) Исследовались распределения оценок параметра формы  и статистик критериев при известном параметре масштаба . Начальное прибли­жение  определялось по методу моментов.

c) Исследовались распределения оценок параметра масштаба  и стати­стик критериев при известном параметре формы . Начальное прибли­жение  определялось по методу моментов.

d) Исследовались распределения оценок и распределения статистик кри­териев согласия при одновременном оценивании двух параметров закона рас­пре­деления Вейбулла или гамма-распределения. В качестве начального прибли­жения  использовались “зашумленные” оценки, получаемые из оценок по методу моментов добавлением некоторой ошибки приближения (ОММ*): , где  – генерировалась по нормальному закону с нулевым математическим ожиданием и среднеквадратичным отклонением 0,1.

            В случае a), когда одновременно оценивались оба параметра закона, зна­чимых отклонений между плотностями законов распределений оценок  и ,  и , как для распределения Вейбулла, так и для гамма-распределения не обнаружено. Соответственно совпадают и распределения статистик  и  для критериев типа Колмогорова и типа  Мизеса. Отличие распределений ОММ приводит к зна­чимому отклонению закона распределения соответствующей статистики  от . Для иллюстрации на рис. 1 представлены плот­ности распределения оценок параметра формы  закона распределения Вей­булла, а на рис. 2 – распределения статистики типа Колмогорова (при одновре­менном оценивании 2-х параметров распределения Вейбулла). Для распределе­ния Вейбулла плотности оценок  и ,  и  практически совпадают. Практически идентичная картина наблюдается в аналогичной ситуации для гамма-рас­пре­деления. Правда, в этом случае ме­жду соответствующими плотностями нет абсолютного совпадения, можно от­метить визуально некоторое отличие, но это отличие статистически не зна­чимо и не сказывается на распределениях соответствующих статистик крите­риев согласия.

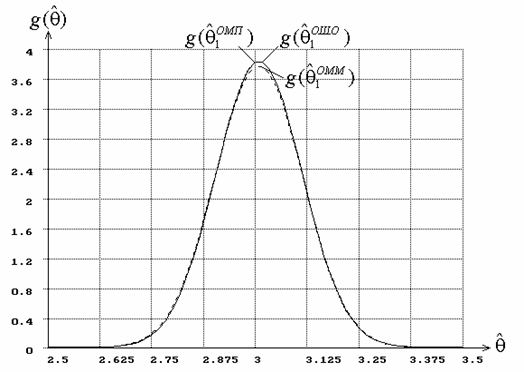
Рис. 1. Плотности распределений оценок параметра  распределения Вейбулла при оценивании двух параметров одновременно.

 

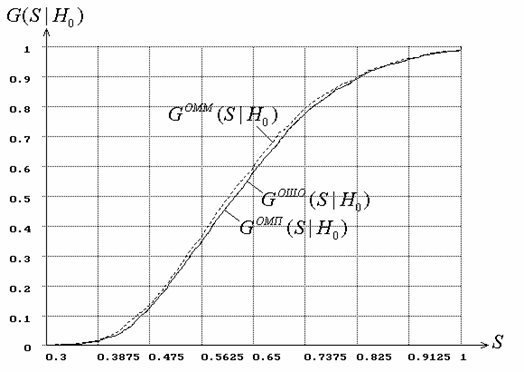
Рис. 2. Распределения статистики типа Колмогорова при вычислении оценок параметров  и  распределения Вейбулла

 

В случае b), когда оценивался только параметр формы  при известном масштабном параметре , между плотностями оценок  и  (и для распределения Вейбулла, и для гамма-распределения) наблюдаются доста­точно значимые раз­личия. На рис. 3 представлены плотности оценок ,  и  для распределения Вейбулла при известном масштабном параметре , а на рис. 4, соответственно, – распределения статистики Колмо­горова , , между которыми наблю­даются столь же значимые различия. На рис. 3 кроме указанных выше плотностей оценок, построенных на основании моделирования, приведена плотность предельного нормального закона  асимптотически эффективной оценки параметра формы  распределения Вейбулла с асимпто­тической дисперсией, опреде­ля­емой соотношением , где количество информации Фишер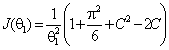а , а  – постоянная Эйлера.

 

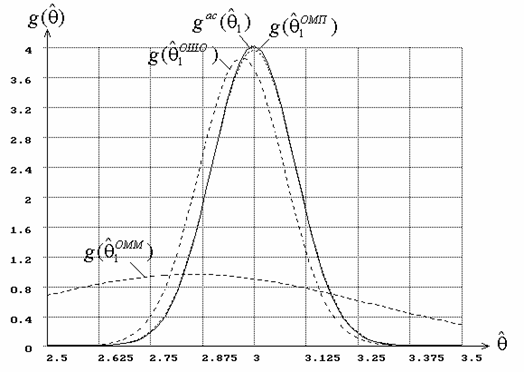
Рис. 3. Плотности распределений оценок параметра  распределения Вейбулла, параметр  полагается известным

 

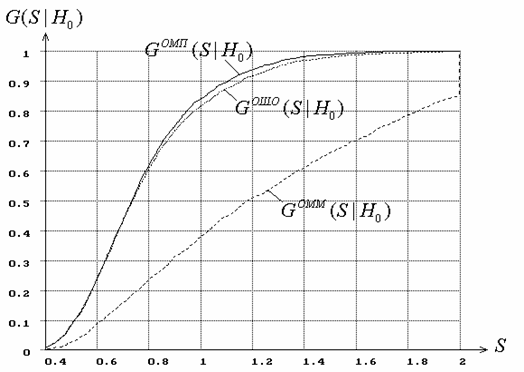
Рис. 4. Распределения статистики Колмогорова при оценивании параметра  распределения Вейбулла

 

В случае c), когда оценивался только масштабный параметр  при из­вестном параметре формы , для гамма-распределения между плот­но­стями оценок  и  наблюдаются значимые раз­личия (см. рис. 5). Это приводит к отличию в распределениях  и  ста­тистики типа Колмогорова (см. рис. 6). Аналогично отличаются и стати­стики типа  Мизеса. На рис. 5 для иллюстрации приведена также плотность нормального закона асимптотически эффективной оценки параметра масштаба  гамма-распределения с асимптотической дисперсией , где . В то же время следует отметить, что в аналогичной ситуации для распределения Вейбулла плот­ности оценок  и  совпадают(!).

 

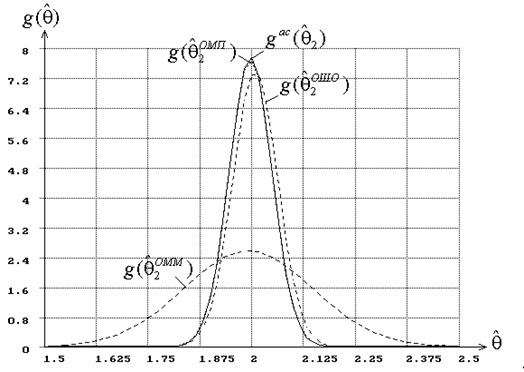
Рис. 5. Плотности распределений оценок параметра  гамма-распределения, параметр  полагается известным

 

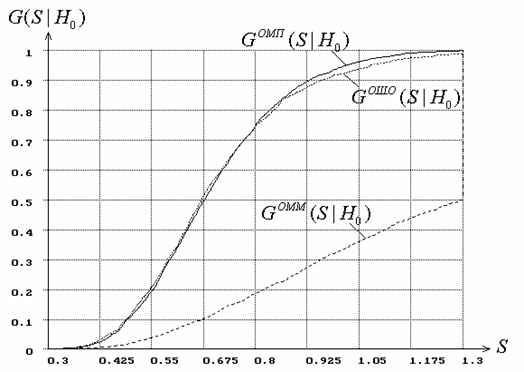
Рис. 6. Распределения статистики Колмогорова при оценивании параметра  гамма-распределения.

 

В случае d) (при одновременном оценивании двух параметров закона и выборе в качестве начального прибли­жения для вычисления оценок методами Ньютона-Рафсона и накопления Рао “зашумленных” оценок ) меж­ду распре­деле­ниями оценок параметра формы ,  и между распреде­лениями оценок параметра масштаба ,  обычно наблюдаются сущест­венные различия (как для распределения Вейбулла, так и для гамма-распреде­ления). Например, на рис. 7 представлены в данной ситуации плотности оценок ,  для распределения Вейбулла, а на рис. 8 – распределения статистики  и  критерия типа  Мизеса.

 

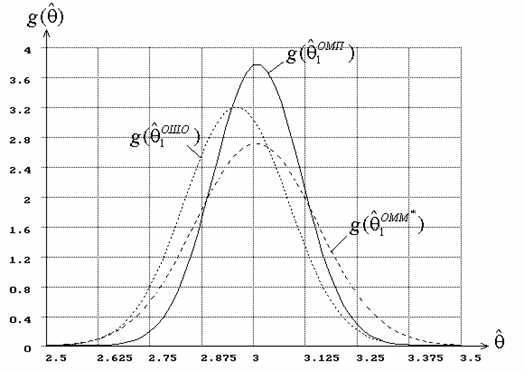
Рис. 7. Плотности распределений оценок параметра  распределения Вейбулла в случае оценивания двух параметров одновременно

 

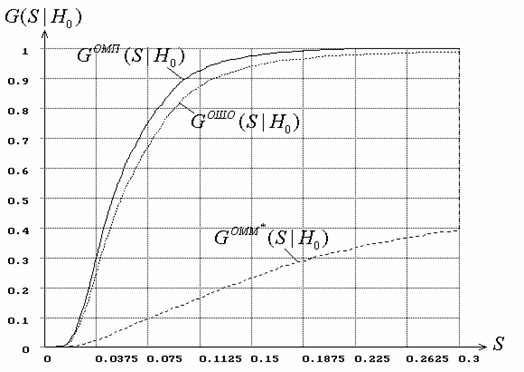
Рис. 8. Распределения статистики типа  Мизеса при вычислении оценок параметров  и  распределения Вейбулла.

 

            Плотности распределений оценок, приводимые на рисунках 1, 3, 5 и 7, представляют собой плотности нормального закона, хорошо аппрокси­миру­ющего эмпирический закон распределения соответствующей оценки. Пара­метры  и  нормального закона 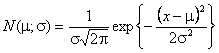, аппро­ксимирующего соответствующее распределение оценок, отражены в табл. 1.

 

Таблица 1

№ рисунка

Параметры нормального закона

 

Рис. 1

  = N(3,0096; 0,1040)

 = N(3,0090; 0,1039)

 = N(3,0090; 0,1056)

 

 

Рис. 3

    = N(2,9983; 0,0993)

  = N(2,9983; 0,1006)

 = N(2,9700; 0,1032)

 = N(2,8516; 0,4162)

 

 

Рис. 5

   = N (1,9977; 0,0516)

  = N (1,9977; 0,0519)

 = N (2,0089; 0,0540)

 = N (1,9922; 0,1558)

 

Рис. 7

  = N(3,0096; 0,1057)

 = N(2,9590; 0,1247)

 = N(3,0070; 0,1470)

 

Примечание: Распределения  и  на рис. 3 и 5, вообще говоря,  являются оценками асимптотических распределений соответственно  и  при объеме наблюдаемых выборок n=500 и числе выборок N=2000. Повторение экспериментов показало, что величины  и , где k – число повторений таких экспериментов, очень быстро сходятся к асимпто­тическим дисперсиям  и  соот­вет­ственно.

 

Выводы

 

На основании проведенных исследований, можно констатировать, что статистические свойства первого приближения итерационного процесса (3) су­щественно зависят от выбранного начального приближения .

 При хороших начальных приближениях, соответствующих условиям теорем в [6,7], статистические свойства ОШ-оценок совпадают со свойствами ОМП. В этом случае совпадают и распределения статистик непараметрических критериев согласия  и .

Если же начальное приближение оказывается недостаточно хорошим, то между законами распределения ОМП и ОШ-оценок (они уже не будут ОШ-оценками, как  это понимается в [7]) появляются значимые различия, которые приводят к значимым же различиям в рас­пределениях статистик  и . Обычно, но не всегда, ОММ оказы­ваются достаточно хоро­шим начальным приближением для ОШ-оценок.

Общий вывод, опирающийся на результаты и свойства итерационного процесса (3), можно сформулировать следующим образом. Если начальное приближение  оказывается в области, в которой логарифм функции правдо­подобия хо­рошо аппроксимируется квадратичной функцией (а это соответст­вует условиям теорем в [6,7]), то статистические свойства получаемых ОМП (3) и ОШ-оценок (4) близки. В этом случае можно при проверке сложных гипотез пользоваться моделями предельных распределений статистик непараметриче­ских критериев согласия, построенных для случая применения ОМП [2,3].

 

Литература

 

1.      Лемешко Б.Ю., Постовалов С.Н. О зависимости распределений статистик      непараметрических критериев и их мощности от метода оценивания пара­метров // Заво­дская лаборатория. Диагностика материалов. – 2001. – Т. 68. – № 7. – С.  (в печати).

2.      Лемешко Б.Ю., Постовалов С.Н. Прикладная статис­тика. Правила проверки согласия опытного распределения с тео­ретическим. Мето­ди­ческие реко­мен­дации. Часть II. Непараметрические критерии. – Новосибирск: Изд-во НГТУ, 1999. – 85 с.

3.      Лемешко Б.Ю., Постовалов С.Н. О распределениях статистик непара­мет­ри­ческих крите­риев согласия при оценивании по выборкам параметров на­блю­даемых законов // Заво­дская лаборатория. 1998. – Т. 65. – № 3. – С. 61-72

4.      Закс Ш. Теория статистических выводов. М.: Мир, 1975. – 776 с.

5.      Джапаридзе К.О. Об упрощенных оценках неизвестных параметров с хоро­шими асимптотическими свойствами // Теория вероятностей и ее примене­ния. – 1974. – Т. XIX. – №2, – С. 335-366.

6.      Боровков А.А. Математическая статистика. – М.: Наука, 1984. – 472 с.

7.      Орлов А.И. О нецелесообразности использования итеративных про­це­дур на­хождения оценок максимального правдоподобия // Заводская лаборатория, 1986. – Т. 52. – № 5. – С. 67-69.

8.      Рао С.Р. Линейные статистические методы и их применения. – М.: Наука, 1968. – 548 с.

9.      Орлов А.И. Методы оценки близости допредельных и предельных распре­де­лений статистик // Заводская лаборатория. 1998. – Т. 64. – № 5. – С. 64-67.

10.  ГОСТ 11.011-83. Правила определения оценок и доверительных границ для параметров гамма-распределения. – М.: Изд-во стандартов, 1984.

11.  Орлов А.И. О критериях Колмогорова и Смирнова // Заводская лаборатория. 1995. – Т. 61. – № 7. – С. 59-61.

12.  Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука, 1983. – 416 с.

 

Приложение:

 

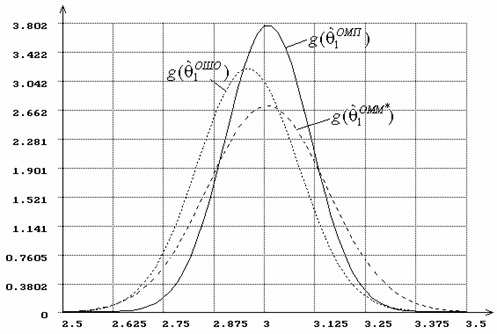
Рис. 9. Плотности распределений оценок параметра  распределения Вейбулла в случае оценивания двух параметров одновременно.

 

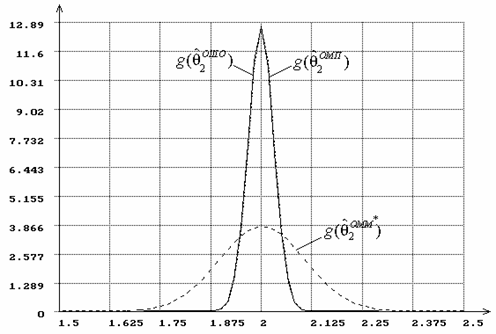
Рис. 10. Плотности распределений оценок параметра  распределения Вейбулла в случае оценивания двух параметров одновременно.

 

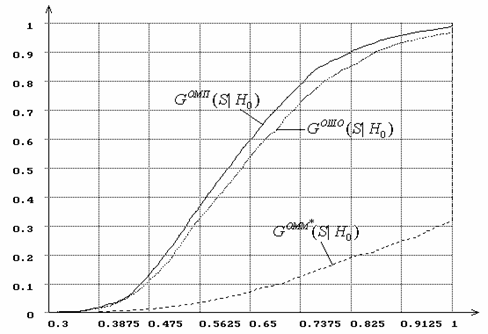
Рис. 11. Распределения статистики типа Колмогорова при вычислении оценок параметров  и  распределения Вейбулла.

 

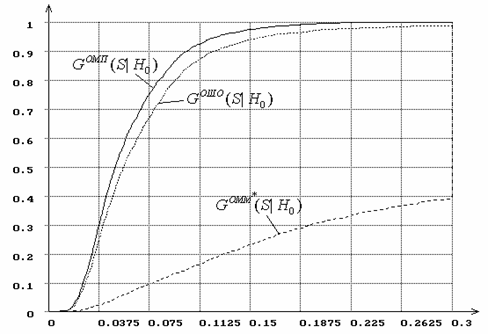
Рис. 12. Распределения статистики типа  Мизеса при вычислении оценок параметров  и  распределения Вейбулла.

 

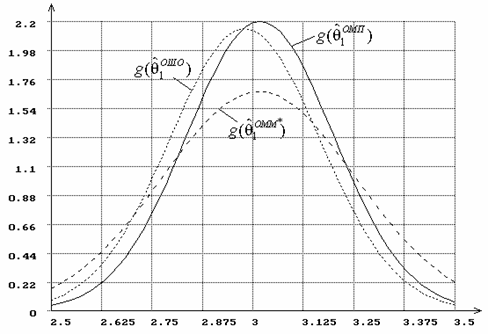
Рис. 13. Плотности распределений оценок параметра  гамма-распределения в случае оценивания двух параметров одновременно.

 

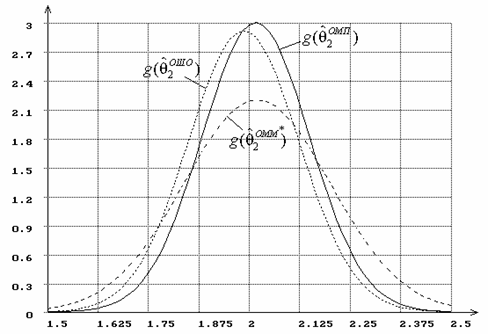
Рис. 14. Плотности распределений оценок параметра  гамма-распределения в случае оценивания двух параметров одновременно.

 

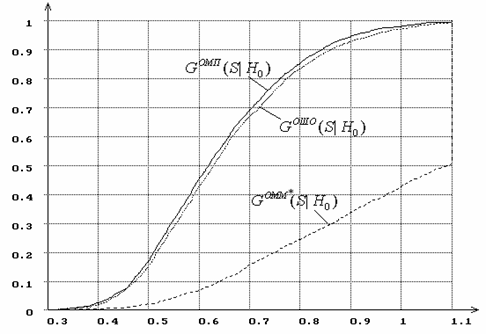
Рис. 15. Распределения статистики типа Колмогорова при вычислении оценок параметров  и  гамма-распределения.

 

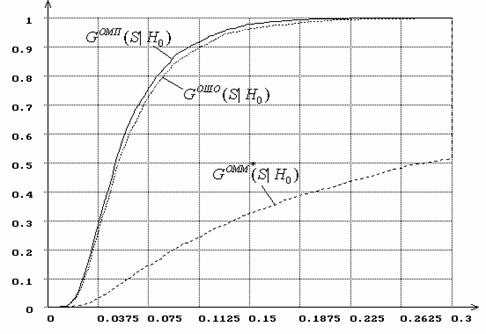
Рис. 16. Распределения статистики типа  Мизеса при вычислении оценок параметров  и  гамма-распределения.

 

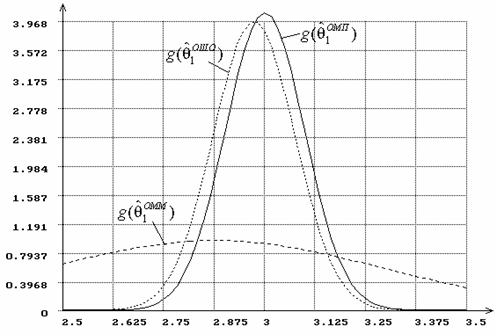
Рис.17. Плотности распределений оценок параметра  распределения Вейбулла, параметр  полагается известным.

 

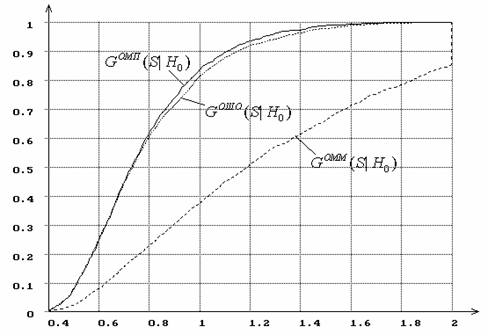
Рис.18. Распределения статистики Колмогорова при оценивании параметра  распределения Вейбулла.

 

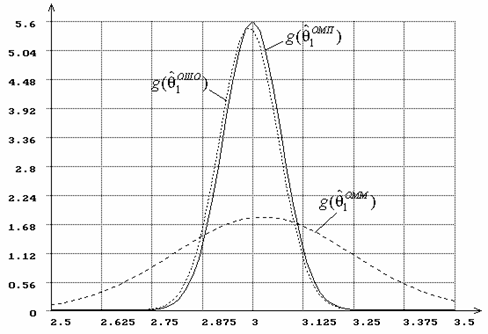
Рис.19. Плотности распределений оценок параметра  гамма-распределения, параметр  полагается известным.

 

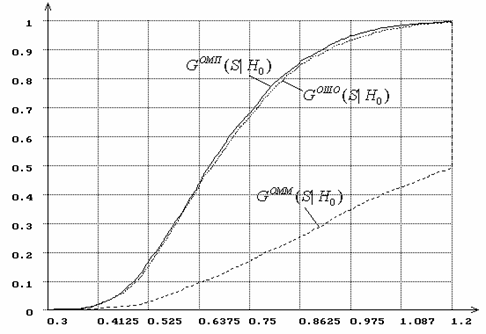
Рис.20. Распределения статистики Колмогорова при оценивании параметра  гамма-распределения.

 

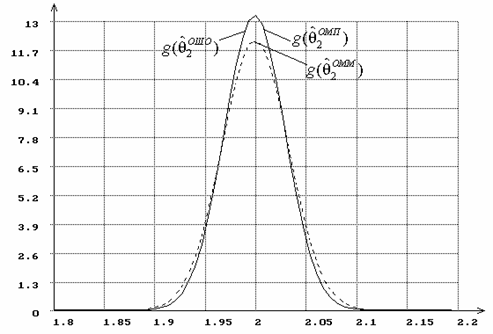
Рис.21. Плотности распределений оценок параметра  распределения Вейбулла, параметр  полагается известным.

 

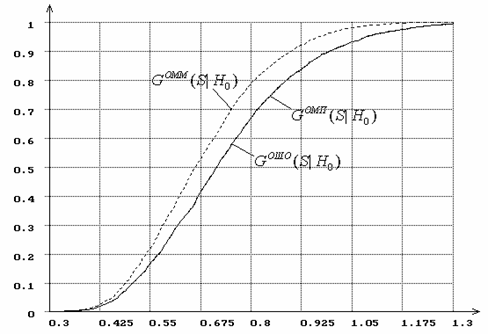
Рис.22. Распределения статистики Колмогорова при оценивании параметра  распределения Вейбулла.

 

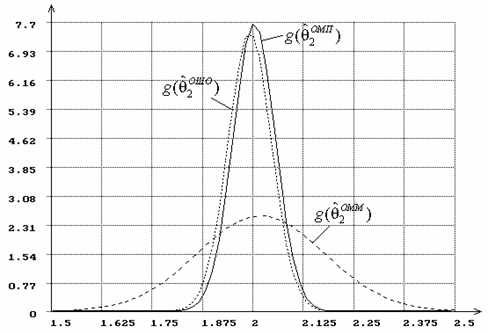
Рис.23. Плотности распределений оценок параметра  гамма-распределения, параметр  полагается известным.

 

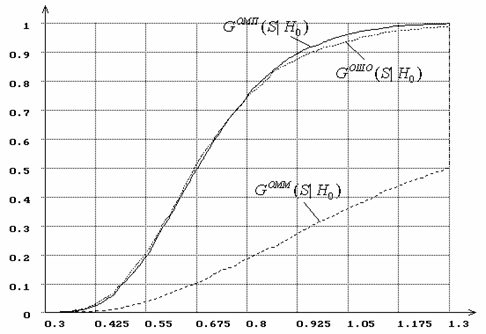
Рис.24. Распределения статистики Колмогорова при оценивании параметра  гамма-распределения.

 

 


[1] Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект 00-01-00913)

 

 

[Содержание]