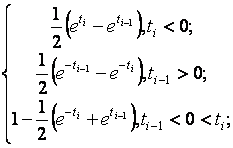
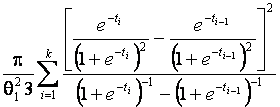
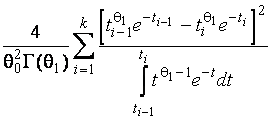
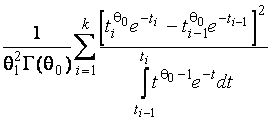
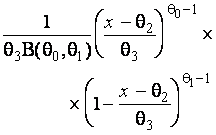
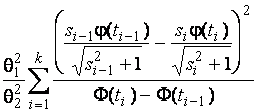
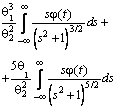
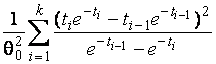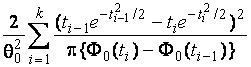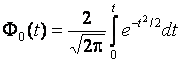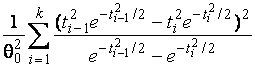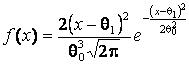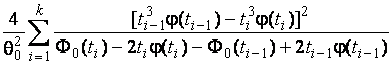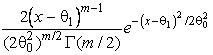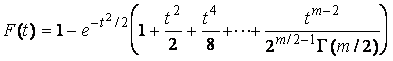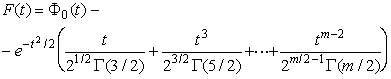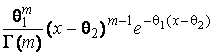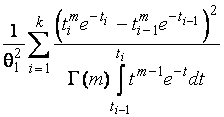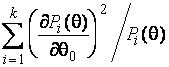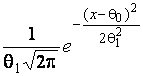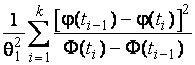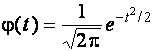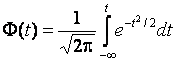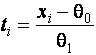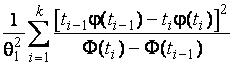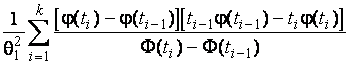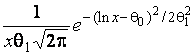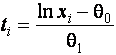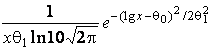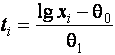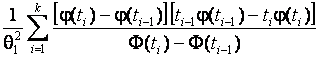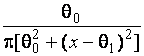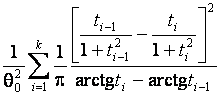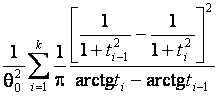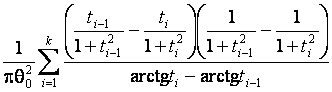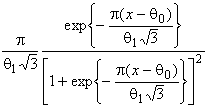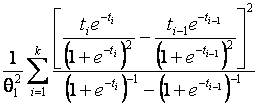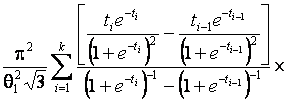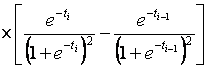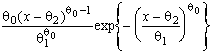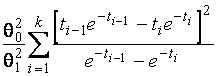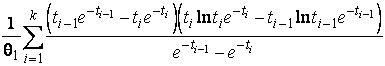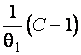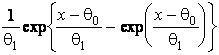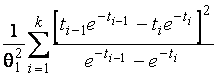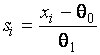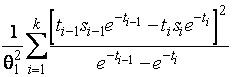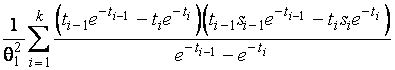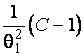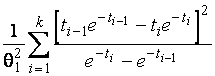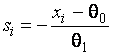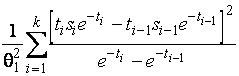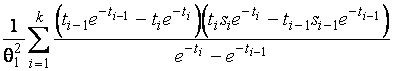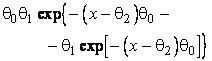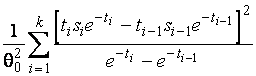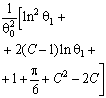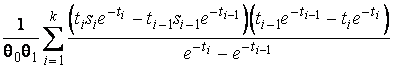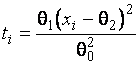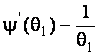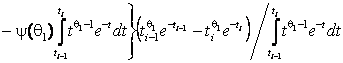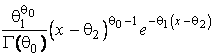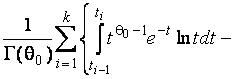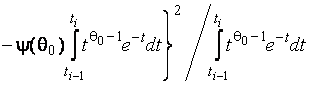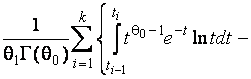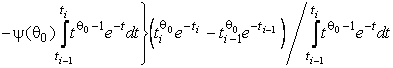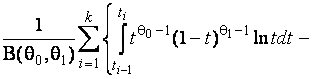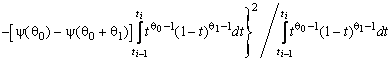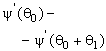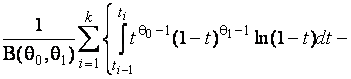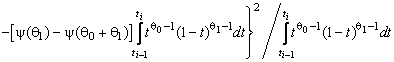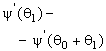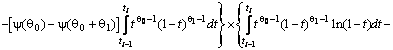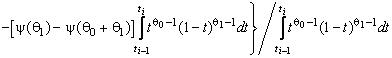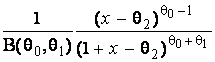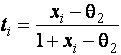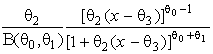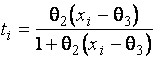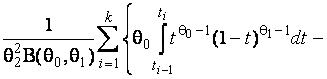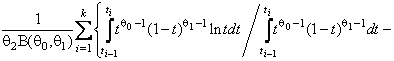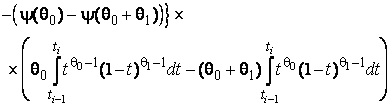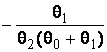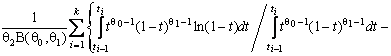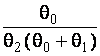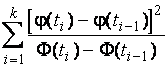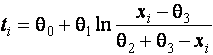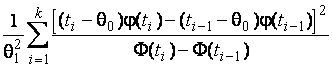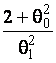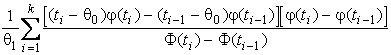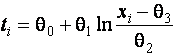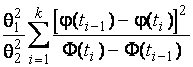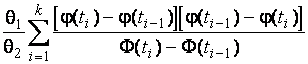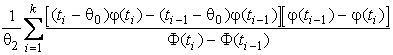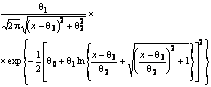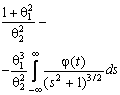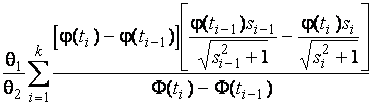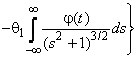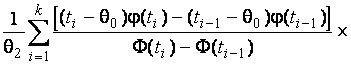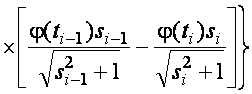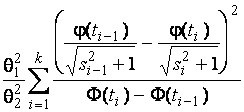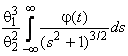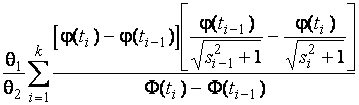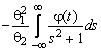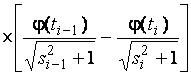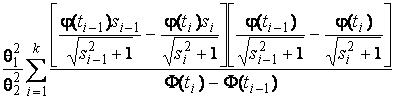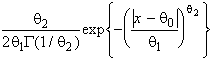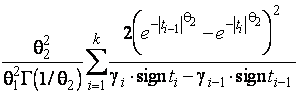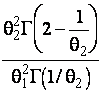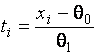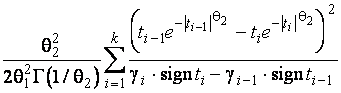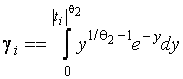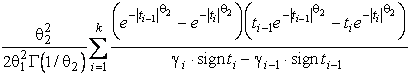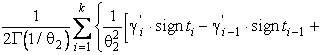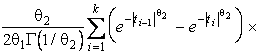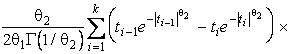–Таблица 3 – Функции плотности распределений, элементы информационных матриц Фишера по группированным и негруппированным наблюдениям, соответствующие таблицы  асимптотически оптимального группирования

	Функция плотности распределения	Параметр распределения	Количество информации Фишера для параметра по наблюдениям		Номер таблицы  АОГ
			группированным	негруппированным
1	Экспоненциальное , ,	q0			А.1	А.2
2	Полунормальное , ,	q0	,		А.6	А.7
3	Рэлея ,	q0			А.3	А.2
4	Максвелла ,	q0			А.4	А.5
5	Модуля нормального вектора , ,	q0	, при четном m при нечетном -	m=4 m=5 m=6 m=7 m=8 m=9	А.8 А.10 А.12 А.14 А.16 А.18	А.9 А.11 А.13 А.15 А.17 А.19
6	Парето , ,	q0			А.1	А.2
7	Эрланга порядка ,				А.54	-
8	Лапласа , ,	q0	,		А.46 А.47	А.48 А.49
9	Нормальное , ,	q0	, ,		А.24	А.25
					А.26	А.27
		q0, q1		0	А.28	А.29
10	Логарифмически (ln) ,	q0			А.24	А.25
	,				А.26	А.27
		q0, q1		0	А.28	А.29
11	Логарифмически (lg)	q0			А.24	А.25
	,				А.26	А.27
		q0 ,q1		0	А.28	А.29
12	Коши , ,	q0			А.36	А.37
					А.38	А.39
				0	А.40
13	Логистическое ,	q0			А.41
					А.42	А.43
				0	А.44	А.45
14	Вейбулла ,	q0			А.20	А.21
	,  - постоянная Эйлера				А.1	А.2
					А.22	А.23
15.	Минимального значения ,	q0			А.1	А.2
	,				А.20	А.21
					А.22	А.23
16	Максимального значения ,	q0			А.30	А.31
	,				А.32	А.33
					А.34	А.35
17	Двойное показательное ,	q0			А.50	А.51
	,				А.1	А.31
					А.52	А.35
18	Накагами	q0			–	–
	, ,				–	–
				0	–	–
19	Гамма-распределение ,	q0			А.53	А.54
					А.55	А.56
					А.57	А.58
20	Бета-распределение 1-го рода	q0			–	–
	,				–	–
					–	–
21	Стандартное бета-распределение 2-го рода	q0	См. соответствующие соотношения для бета-распределения 1-го рода	–”–	–	–
	,		См. соответствующие соотношения для бета-распределения 1-го рода	–”–	–	–
			См. соответствующие соотношения для бета-распределения 1-го рода	–”–	–	–
22	Бета-распределение 2-го рода	q0	См. соответствующие соотношения для бета-распределения 1-го рода	–”–	–	–
	,		См. соответствующие соотношения для бета-распределения I-го рода	–”–	–	–
			См. соответствующие соотношения для бета-распределения I-го рода	–”–	–	–
					–	–
					–	–
					–	–
23	Распределение Sb-Джонсона ,	q0		1	А.24	А.25
					А.26	А.27
					А.28	А.29
24	Распределение Sl-Джонсона	q0		1	А.24	А.25
	,				А.26	А.27
					А.28	А.29
					А.24	А.25
					–	–
					–	–
25	Распределение Su-Джонсона	q0		1	А.24	А.25
					–	–
					А.28	А.29
					–	–
					–	–
					–	–
					–	–
					–	–
					–	–
					–	–
26	Класс экспоненциальных распределений ,	q0			–	–
	,				–	–
	,			0	–	–
				0	–	–
				0	–	–
					–	–

[Предыдущая][Содержание][Следующая]