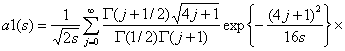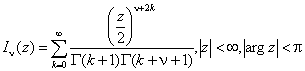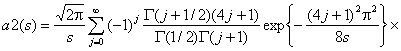2.2.3 Критерии w²

         В критериях типа w² расстояние между гипотетическим и истинным распределениями рассматривают в квадратичной метрике.

         Проверяемая гипотеза H₀ имеет вид [3]

                           (13)

при альтернативной гипотезе

,                          (14)

где E[^.]  - оператор математического ожидания, y(t) - заданная на отрезке 0£t£1 неотрицательная функция, относительно которой предполагают, что y(t), ty(t), t²y(t) интегрируемы на отрезке 0£t£1 [4]. Статистику критерия [3] выражают соотношением

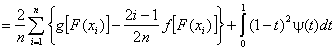,        (15)

где

,    .

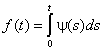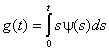         При выборе y(t) º1 для критерия w² Мизеса получают статистику вида (статистику Крамера-Мизеса-Смирнова)

,                        (16)

которая при простой гипотезе в пределе подчиняется закону с функцией распределения a1(S), имеющей вид [3]

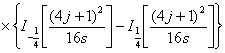,                       (17)

где  - модифицированные функции Бесселя,

.                   (18)

         При выборе y(t) º1/t(1-t)  для критерия W² Мизеса статистика приобретает вид (статистика Андерсона-Дарлинга)

.  (19)

В пределе эта статистика подчиняется закону с функцией распределения a2(S), имеющей вид [3]

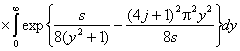.                              (20)

         Гипотезы о согласии не отвергают, если выполнены неравенства

P{S_w> S_w^*}=1-a1(S_w^*)>a и  P{S_W> S_W^*}=1-a2(S_W^*)>a.

[Предыдущая][Содержание][Следующая]