2.3.8 Зависимость распределений статистик непараметрических критериев от конкретных значений параметра

         В некоторых случаях предельные распределения G(S|H₀) рассматриваемых статистик при проверке сложных гипотез зависят от конкретных значений параметров распределения, с которым проверяют согласие. В частности, распределения G(S|H₀)  непараметрических критериев согласия в случае проверки согласия с гамма-распределением с плотностью

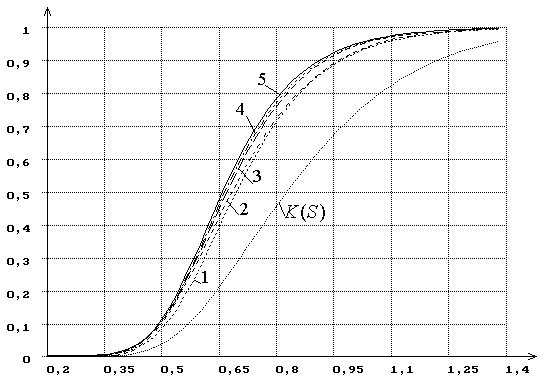
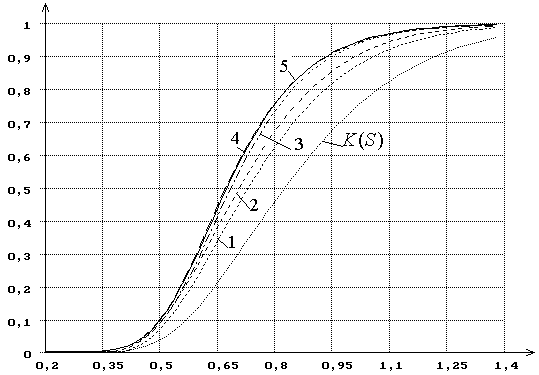
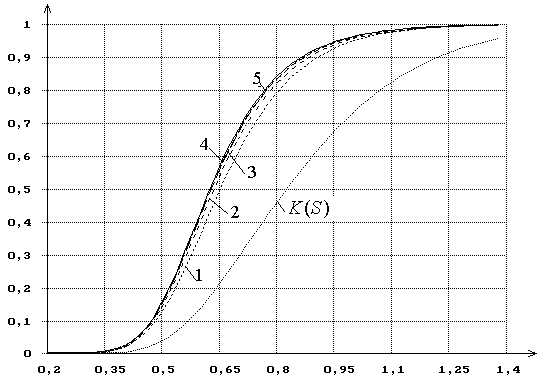
зависят от его параметра формы q₀. Для иллюстрации приведены лишь распределения G(S|H₀)  статистики Колмогорова S_K. На рисунке 21 показаны распределения статистики при оценивании по выборке параметра формы, на рисунке 22 - масштабного параметра, на рисунке 23 - двух параметров распределения. На этих рисунках цифрами по порядку помечены функции распределения статистики: 1 – при q₀=0,5; 2 – при q₀=1,0; 3 – при q₀=2,0; 4 – при q₀=3,0; 5 – при q₀=5,0. Для сравнения приведена функция распределения Колмогорова K(S).

Рисунок 21 – Функции распределения статистики S_K Колмогорова при вычислении ОМП параметра формы гамма-рапределения: K(S) - функция распределения Колмогорова

Рисунок 22 – Функции распределения статистики S_K Колмогорова при вычислении ОМП масштабного параметра гамма-рапределения. K(S) - функция распределения Колмогорова

Рисунок 23 – Функции распределения статистики S_K Колмогорова при оценивании методом максимального правдоподобия одновременно двух параметров гамма-рапределения. K(S) - функция распределения Колмогорова

С ростом q₀ предельные распределения статистик сходятся к предельным распределениям статистик для выборок из нормального закона. При значениях q₀>5 эмпирические распределения статистик при оценивании двух параметров практически совпадают и хорошо согласуются с распределением соответствующей статистики для нормального закона.

            Общая картина принципиально сохраняется и для распределений других непараметрических статистик.

[Предыдущая][Содержание][Следующая]