2.3.7 Метод оценивания и мощность непараметрических критериев согласия

         При использовании MD-оценок, минимизирующих статистику критерия, эмпирические распределения G(S_n|H₀), соответствующие различным гипотезам H₀, имеют минимальный разброс, что означает определенную “свободу от распределения” для рассматриваемых критериев. Этот факт говорит за использование MD-оценок при проверке сложных гипотез. Но если исследовать мощность рассматриваемых критериев при различных методах оценивания, то оказывается, что максимальную мощность непараметрические критерии при близких альтернативах имеют в случае оценивания параметров методом максимального правдоподобия.

Способность применяемого критерия различать альтернативы H₀ и H₁ зависит от его мощности 1-b при заданном уровне значимости a, то есть от того, насколько существенно отличаются распределения статистики G(S_n|H₀) и G(S_n|H₁). При одинаковых объемах выборок n отличие распределений G(S_n|H₀) и G(S_n|H₁) в случае использования ОМП более значительно, а, следовательно, критерий оказывается более мощным, чем в случае использования MD-оценок.

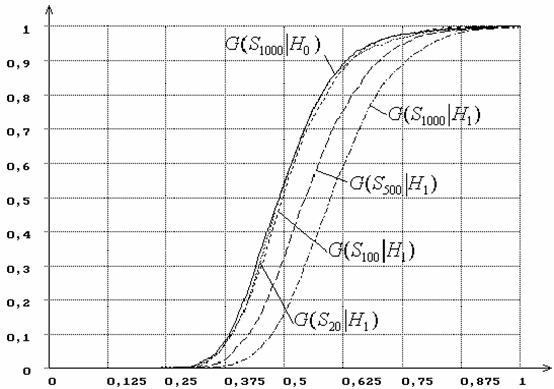
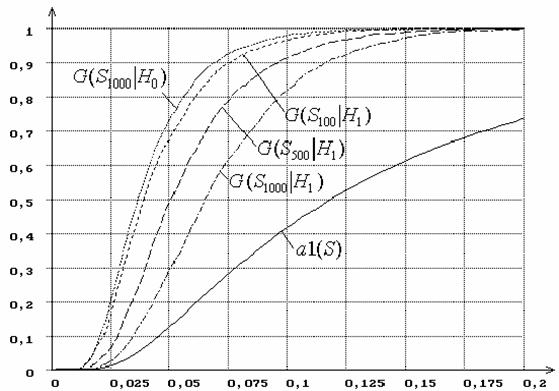
Например, рисунок 17 иллюстрирует зависимость от n распределений G(S_n|H₁) статистики S_K Колмогорова при проверке сложной гипотезы при паре альтернатив H₀ - нормальное распределение, H₁ - логистическое и использовании MD-оценок S_K, а рисунок 18 – зависимость от n распределений G(S_n|H₁) статистики S_w Крамера-Мизеса-Смирнова при использовании MD-оценок S_w.

Сравнивая рисунок 17 с рисунком 6, а рисунок 18 с рисунком 8, можно убедиться, что в случае использования метода максимального правдоподобия мощность критериев типа Колмогорова и типа w² Мизеса много выше, чем при использовании соответствующих MD-оценок. Аналогичная картина справедлива и для критерия типа W² Мизеса со статистикой S_W  Андерсона-Дарлинга.

Рисунок 17 – Зависимость от n распределений G(S_n|H₁) статистики S_K Колмогорова при сложной гипотезе (H₀ - нормальное распределение, H₁ - логистическое, MD-оценки S_K): n = 20, 100, 500, 1000

Рисунок 18 – Зависимость от n распределений G(S_n|H₁) статистики S_w Крамера-Мизеса-Смирнова при сложной гипотезе (H₀ - нормальное распределение, H₁ - логистическое, MD-оценки S_w): n = 100, 500, 1000

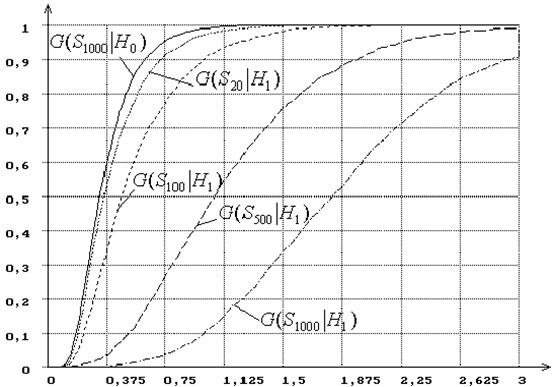
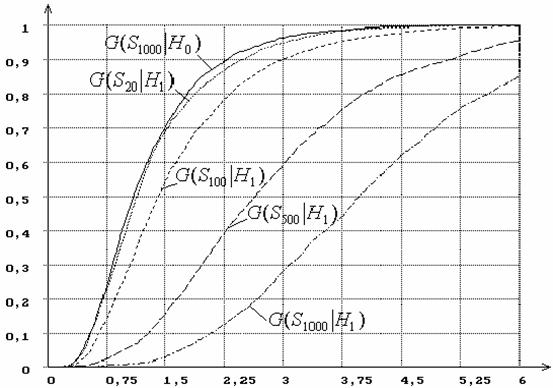
Для того чтобы сравнить по мощности непараметрические критерии согласия для рассматриваемой пары близких гипотез H₀ и H₁ при использовании ОМП, на рисунке 19 приведены распределения G(S₁₀₀₀|H₁) и G(S_n|H₁) при n= 20, 100, 500, 1000 для статистики S_W  Андерсона-Дарлинга, а на рисунке 20 для статистики S_m Смирнова.

Рисунок 19 – Зависимость от n распределений G(S_n|H₁) статистики S_W  Андерсона-Дарлинга при сложной гипотезе (H₀ - нормальное распределение, H₁ - логистическое, ОМП): n = 20, 100, 500, 1000

Анализируя распределения на рисунках 6, 8, 19 и 20, можно заметить, что наиболее мощным для данной пары гипотез является критерий W² со статистикой S_W  Андерсона-Дарлинга, затем критерий w² со статистикой S_w Крамера-Мизеса-Смирнова, далее критерий Колмогорова со статистикой S_K и на последнем месте критерий Смирнова со статистикой S_m. Данное наблюдение о порядке предпочтения критериев хорошо согласуется с опытом их применения.

Почему мощность рассматриваемых критериев при проверке близких гипотез в случае ОМП выше, чем при MD-оценках, достаточно логично объясняет следующая версия. Использование MD-оценок, минимизирующих статистику критерия, приводит к распределению G(S|H₀) с меньшим параметром масштаба (к более крутой функции распределения), чем в случае ОМП. Но с другой стороны, MD-оценки в отличие от ОМП являются робастными, они менее чувствительны к малым отклонениям выборки от предполагаемого закона распределения. Поэтому функция распределения G(S_n|H₁) оказывается еще более крутой по отношению к аналогичному распределению при использовании ОМП.

Рисунок 20 – Зависимость от n распределений G(S_n|H₁) статистики S_m Смирнова при сложной гипотезе (H₀ - нормальное распределение, H₁ - логистическое, ОМП): n = 20, 100, 500, 1000

[Предыдущая][Содержание][Следующая]