2.3.5
Влияние объема выборки на мощность непараметрических критериев при простых и
сложных гипотезах
Способность различать близкие гипотезы зависит от
того, насколько сильно различаются распределения G(Sn|H0) и G(Sn|H1).
Предложены к рассмотрению
две близкие гипотезы: H0 - нормальное распределение с плотностью 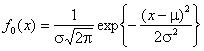 и
параметрами m=0, s=1; H1 -
логистическое с такими же параметрами
m=0,
s=1 и плотностью
и
параметрами m=0, s=1; H1 -
логистическое с такими же параметрами
m=0,
s=1 и плотностью 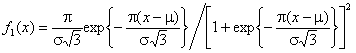 . О
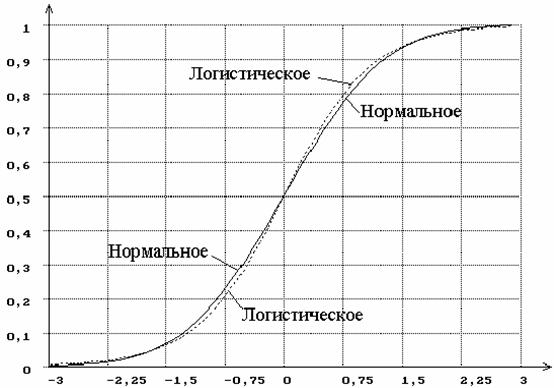
близости этих законов распределения можно судить по рисунку 4,
на котором представлены их функции распределения. Рисунок 5
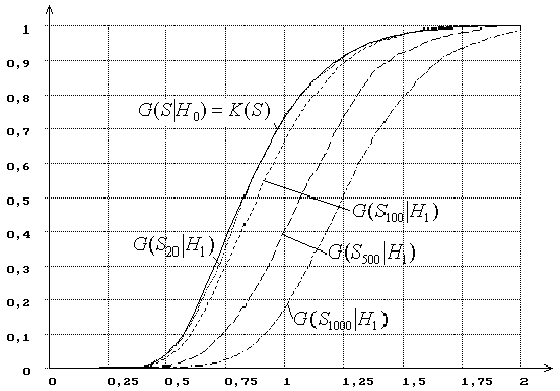
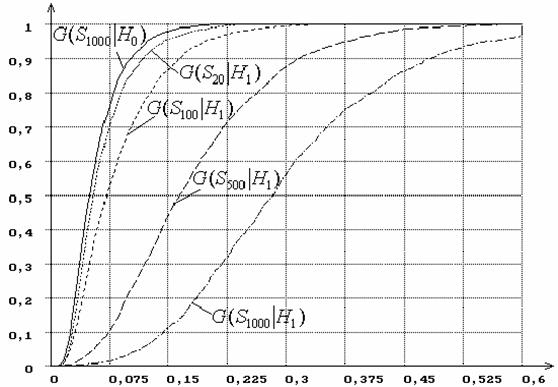
иллюстрирует зависимость от n распределений G(Sn|H1) статистики SK Колмогорова при проверке простой (n
= 20, 100, 500, 1000), а рисунок
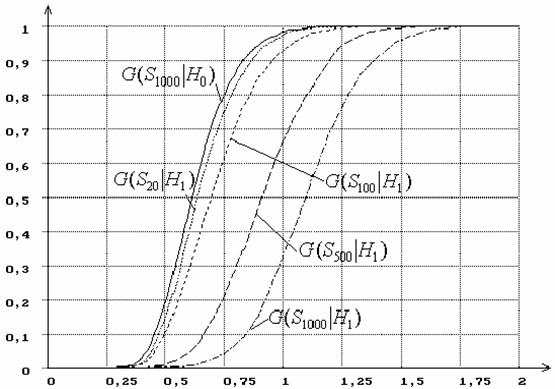
6 – при проверке сложной гипотезы H0 (при использовании ОМП).
. О
близости этих законов распределения можно судить по рисунку 4,
на котором представлены их функции распределения. Рисунок 5
иллюстрирует зависимость от n распределений G(Sn|H1) статистики SK Колмогорова при проверке простой (n
= 20, 100, 500, 1000), а рисунок
6 – при проверке сложной гипотезы H0 (при использовании ОМП).
Рисунок 4 – Функции распределения нормального и логистического законов
Рисунок 5 – Зависимость от n распределений G(Sn|H1) статистики SK Колмогорова при простой гипотезе (H0 - нормальное
распределение, H1 - логистическое): n= 20, 100, 500, 1000
Рисунок 6 – Зависимость от n распределений G(Sn|H1) статистики SK Колмогорова при сложной гипотезе (H0 -
нормальное распределение, H1 - логистическое, ОМП): n= 20, 100, 500, 1000
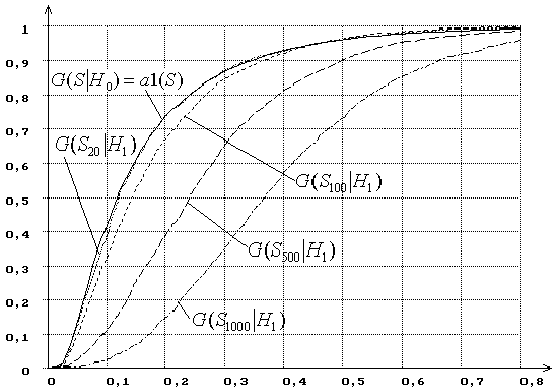
На рисунках 7-8 для
сравнения представлены распределения G(Sn|H1) статистики
Sw при проверке
простой (рисунок 7) и сложной гипотезы (рисунок
8) для тех же самых альтернатив H0 и H1. Для данной пары альтернатив в случае проверки
сложной гипотезы критерий согласия типа w2 Крамера-Мизеса-Смирнова обладает несколько
большей мощностью при различении близких гипотез, чем критерий типа
Колмогорова, а в случае простых – наоборот.
С точки зрения
практического использования критериев важны два момента, которые подтверждены
результатами исследований и хорошо иллюстрированы рисунками 5-8. Во-первых,
очевидно, что при малых выборках пытаться различать с помощью
непараметрических критериев согласия близкие гипотезы (особенно простые)
абсолютно бесполезно. Во-вторых, мощность непараметрических критериев при
проверке сложных гипотез при тех же объемах выборок n всегда существенно выше, чем при проверке простых.
При проверке простых
гипотез неaпараметрические критерии типа Колмогорова, Смирнова, w2 и W2 Мизеса уступают по
мощности критериям типа c2, особенно, если в
последних используется асимптотически оптимальное группирование [31]-[34]. Но при проверке сложных гипотез
непараметрические критерии оказываются более мощными. Для того чтобы
воспользоваться их преимуществами, надо только знать распределение G(S|H0) при проверяемой сложной
гипотезе.
Рисунок 7 – Зависимость от n распределений G(Sn|H1) статистики Sw Крамера-Мизеса-Смирнова при простой гипотезе (H0 -
нормальное распределение, H1 -
логистическое): n =
20, 100, 500, 1000
Рисунок 8 – Зависимость от n распределений G(Sn|H1) статистики Sw Крамера-Мизеса-Смирнова при сложной гипотезе (H0 -
нормальное распределение, H0 -
логистическое, ОМП): n =
20, 100, 500, 1000
[Предыдущая][Содержание][Следующая]