2.3.6
Влияние метода оценивания на распределения статистик непараметрических
критериев при сложных гипотезах
Распределения статистик
критериев согласия существенно зависят от метода оценивания параметров, то
есть каждому типу оценок при конкретной сложной проверяемой гипотезе
соответствует свое предельное распределение G(S|H0) статистики.
В данном случае по вполне очевидным причинам при проверке сложных гипотез
сравним результаты использования ОМП и
MD-оценок. MD-оценки получаются при
минимизации некоторого расстояния между эмпирической и теоретической функцией
распределения. Оценки максимального правдоподобия предпочтительны благодаря
своим асимптотическим свойствам [35], [36], а в случае MD-оценок может минимизироваться
значение статистики, используемой в критерии.
ОМП вычисляют в результате максимизации по q функции
правдоподобия
или ее логарифма
Чаще всего в случае
скалярного параметра ОМП определяют как решение уравнения, а в случае
векторного параметра – как решение системы уравнений правдоподобия вида
где m –
размерность вектора параметров q. В общем случае эта
система нелинейна и, за редким исключением, решаема только численно.
При практическом
использовании критериев необходимо иметь в виду следующее. В данном случае, как
и в [20]-[24], при построении распределений
статистик и исследовании их зависимости от метода оценивания ОМП вычисляли как
решение системы (23). Если использовать грубые приближения
ОМП, то это соответственно отражается на распределениях статистик и свойствах
критериев.
При вычислении MD-оценок
минимизируется соответствующее расстояние между эмпирическим и теоретическим
распределениями. При использовании статистики Колмогорова SK в качестве оценки
вектора параметров q выбирают
значения, минимизирующие эту статистику:
(MD-оценки SK). Аналогично, при
использовании статистики Sw минимизируется по
q статистика Sw:
(MD-оценки Sw). При использовании
статистики SW –
(MD-оценки SW).
Вид используемой оценки
оказывает существенное влияние на распределения статистик критериев согласия.
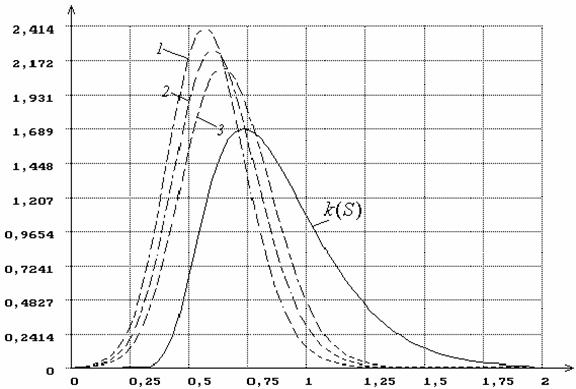
Степень влияния метода оценивания на распределение статистики иллюстрирует рисунок 9, на котором показаны полученные в результате
моделирования плотности распределения g(Sn|H0) статистики
критерия типа Колмогорова SK при
вычислении оценок параметра сдвига нормального распределения тремя различными
методами: минимизацией статистики SK,
минимизацией статистики Sw и методом максимального
правдоподобия. Функция плотности распределения Колмогорова обозначена на
рисунке как k(S).
Рисунок 9 – Плотности
распределения g(Sn|H0) статистики
SK при проверке сложной
гипотезы (H0 - нормальный закон,
оценивается сдвиг: 1 - с использованием MD-оценок SK , 2 - MD-оценок
Sw , 3 – ОМП).
k(S) - плотность
распределения Колмогорова
При использовании ОМП распределения статистик сильно зависят от соответствующего
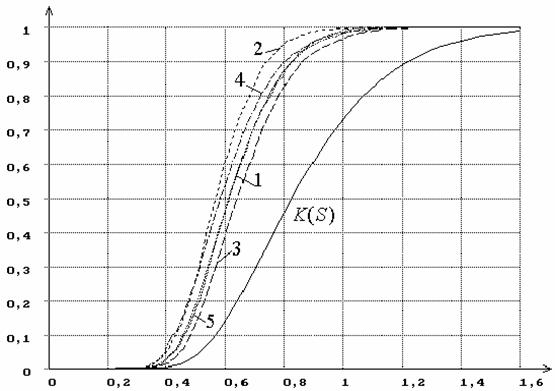
проверяемой гипотезе H0 закона F(x,q). На рисунке 10 приведены
эмпирические распределения G(Sn|H0) статистики Колмогорова SK,
когда при проверке сложной гипотезы два параметра закона, соответствующего
гипотезе H0, оценивали с использованием метода максимального
правдоподобия. При этом на рисунке показаны распределения статистики G(Sn|H0), когда
гипотеза H0 соответствует законам: нормальному,
логистическому, Лапласа с плотностью ![]() ,
распределению наименьшего значения с плотностью
,
распределению наименьшего значения с плотностью 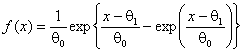 , распределению
Коши с плотностью
, распределению
Коши с плотностью ![]() .
.
Рисунок 10 – Распределения G(Sn|H0) статистики Колмогорова SK при
оценивании двух параметров закона, соответствующего гипотезе H0 (здесь
и далее: 1 – нормального, 2 – логистического, 3 – Лапласа, 4 – наименьшего
значения, 5 – Коши), при использовании ОМП. K(S) - функция
распределения Колмогорова
При использовании MD-оценок, минимизирующих статистику применяемого
критерия согласия, влияние закона F(x,q), соответствующего проверяемой гипотезе H0 проявляется
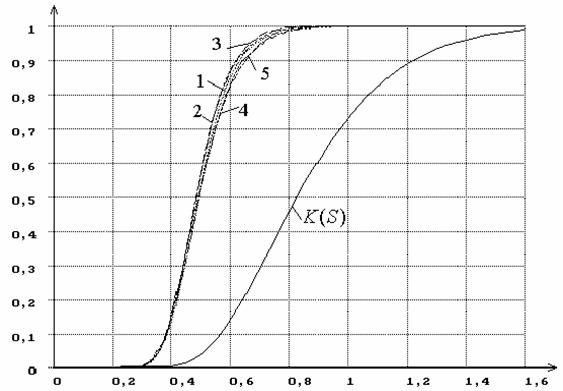
менее значительно. На рисунке 11 показаны распределения
G(Sn|H0) той
же статистики SK при проверке тех же гипотез, но с использованием
MD-оценок параметров, полученных минимизацией по параметрам
статистики SK.
Рисунок 11 – Распределения G(Sn|H0) статистики Колмогорова SK при
оценивании двух параметров закона, соответствующего гипотезе H0, при
использовании MD-оценок SK.
K(S) - функция
распределения Колмогорова, предельная при простой гипотезе
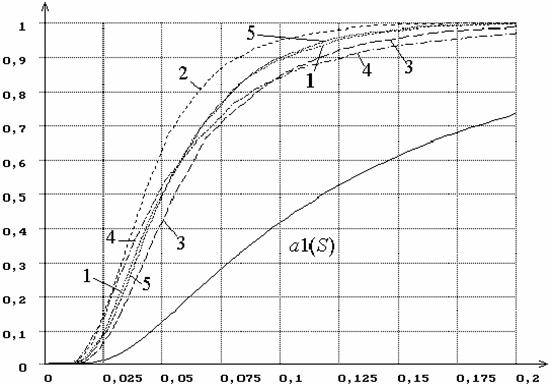
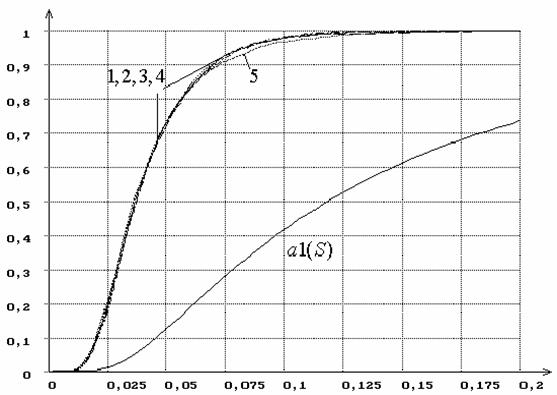
На рисунке 12 приведены распределения статистики Sw для аналогичных гипотез H0 при
использовании ОМП, а на рисунке 13 – при использовании MD-оценок, минимизирующих по параметрам статистику Sw .
При использовании MD-оценок,
минимизирующих по параметрам статистику Sw , эмпирические распределения смоделированных
распределений G(Sn|H0) практически совпадают для законов нормального,
логистического, Лапласа, наименьшего значения, максимального значения с
плотностью 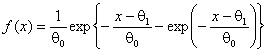 , распределения Вейбулла с плотностью
, распределения Вейбулла с плотностью 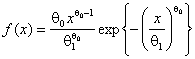 и
хорошо аппроксимируются логарифмически нормальным законом с плотностью
и
хорошо аппроксимируются логарифмически нормальным законом с плотностью ![]() и
параметрами m=-3,2702; s=0,4719.
и
параметрами m=-3,2702; s=0,4719.
Распределения статистик критериев согласия при использовании MD-оценок (как и в случае использования ОМП) существенно
зависят от того, какой параметр оценивался. На рисунке 14
показаны распределения G(Sn|H0) статистики Sw Крамера-Мизеса-Смирнова при использовании MD-оценок Sw и оценивании масштабного параметра закона,
соответствующего гипотезе H0. На рисунке 15 представлены
аналогичные распределения статистик, но при оценивании для тех же распределений
параметра сдвига. Распределения статистик в случае оценивания параметра сдвига
распределения максимального значения и масштабного параметра распределения
Вейбулла совпадают с распределением статистики для распределения минимального
значения.
Рисунок 12 – Распределения G(Sn|H0) статистики Sw Крамера-Мизеса-Смирнова при оценивании двух
параметров закона, соответствующего гипотезе H0, при использовании ОМП. a1(S)- функция
распределения, предельная при простой гипотезе
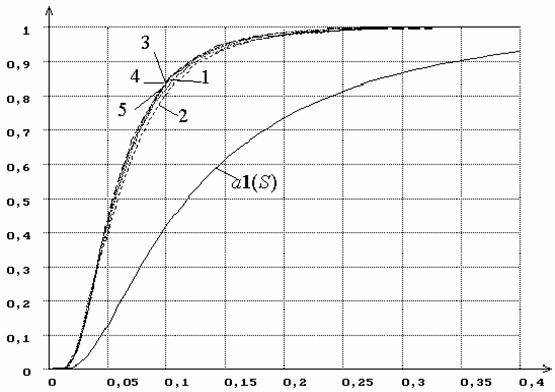
Если обратить внимание
на рисунок 16, на котором отображены распределения G(Sn|H0) статистики
Sw при проверке согласия с распределениями
экспоненциальным ![]() , полунормальным
, полунормальным ![]() , Рэлея
, Рэлея
![]() , Максвелла
, Максвелла 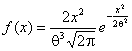 , модуля m
-мерного (m=5) нормального вектора
, модуля m
-мерного (m=5) нормального вектора ![]() при
оценивании масштабного параметра соответствующего закона с использованием MD-оценок Sw , то можно заметить, что распределения статистик
близки к приведенным на рисунке 15. Распределения
статистик, показанные на рисунке 16, например, достаточно
хорошо аппроксимируются логарифмически нормальным законом с параметрами m=-2,8484; s=0,5669.
при
оценивании масштабного параметра соответствующего закона с использованием MD-оценок Sw , то можно заметить, что распределения статистик
близки к приведенным на рисунке 15. Распределения
статистик, показанные на рисунке 16, например, достаточно
хорошо аппроксимируются логарифмически нормальным законом с параметрами m=-2,8484; s=0,5669.
Рисунок 13 – Распределения G(Sn|H0) статистики Sw Крамера-Мизеса-Смирнова при оценивании
двух параметров закона, соответствующего гипотезе H0, при MD-оценках
Sw
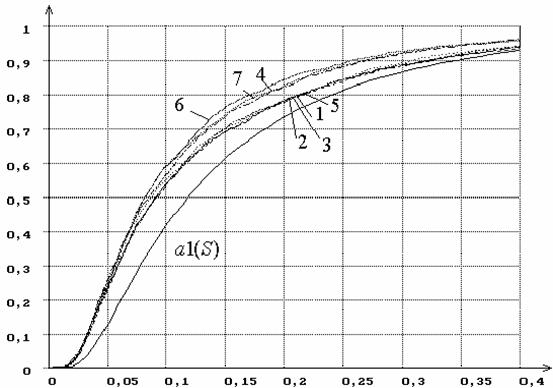
Рисунок 14 – Распределения G(Sn|H0) статистики Sw Крамера-Мизеса-Смирнова при оценивании масштабного
параметра закона, соответствующего гипотезе H0 (6 –максимального значения, 7 – Вейбулла,
параметр формы), при использовании MD-оценок
Sw
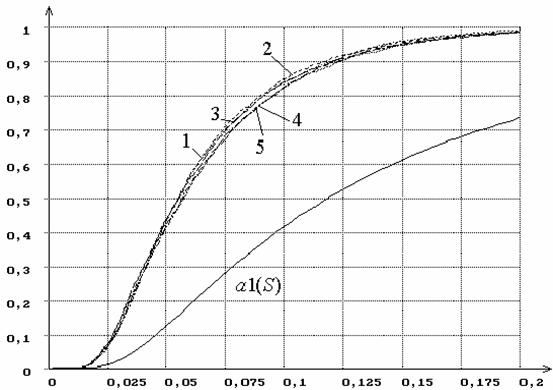
Рисунок 15 – Распределения G(Sn|H0) статистики Sw Крамера-Мизеса-Смирнова при оценивании
параметра сдвига, соответствующего гипотезе H0, при MD-оценках
Sw
Рисунок 16 – Распределения G(Sn|H0) статистики Sw Крамера-Мизеса-Смирнова при оценивании
масштабного параметра закона, соответствующего гипотезе H0 (1
– экспоненциального, 2 – полунормального, 3 – Рэлея, 4 – Максвелла, 5 –
модуля 5-мерного нормального вектора), при использовании MD-оценок Sw
Таким образом, применяя непараметрические критерии
согласия, следует непременно учитывать используемый метод оценивания. При этом
в случае метода максимального правдоподобия распределения статистик G(S|H0) очень
сильно зависят от закона, соответствующего гипотезе H0. Разброс распределений G(S|H0) при использовании MD-оценок, минимизирующих статистику критерия, зависит
от закона F(x,q), соответствующего гипотезе H0, в
существенно меньшей степени.
[Предыдущая][Содержание][Следующая]