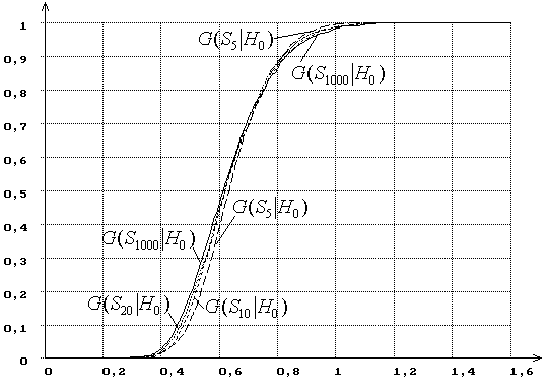2.3.4 Влияние объема выборки на распределения статистик непараметрических критериев при простых и сложных гипотезах

            В случае проверки простых гипотез предельными распределениями статистик критериев Колмогорова и Смирнова можно пользоваться при n>20 [3]. Исследование методами статистического моделирования зависимости распределений статистик всех рассматриваемых здесь непараметрических критериев от объема выборки при проверке различных как простых, так и сложных гипотез показывает, что это справедливо во всех случаях.

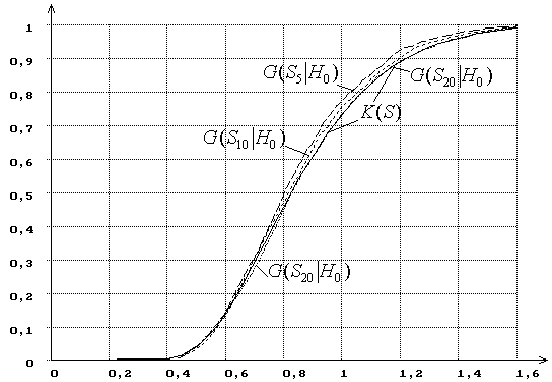
            Например, рисунок 1 иллюстрирует, как при увеличении объема выборки (n =5, 10, 20) меняется распределение G(S_n|H₀) статистики Колмогорова S_K в случае проверки простой гипотезы о принадлежности выборки нормальному закону. На этом рисунке отражено также предельное распределение статистики – функция распределения Колмогорова K(S). Эмпирические распределения G_N(S_n|H₀)   при больших n практически сливаются с K(S), и на рисунке они не показаны. Как видно, при малых n распределение существенно отличается от предельного, но уже при n ³ 15–20 ошибка при вычислении вероятности “согласия” P{S> S^*} оказывается достаточно малой.

Рисунок 1 – Зависимость от n распределений G(S_n|H₀)   статистики S_K Колмогорова при простой гипотезе (H₀ - нормальное распределение): n = 5, 10, 20. K(S) – функция предельного распределения Колмогорова

Та же самая картина наблюдается в случае проверки сложных гипотез о согласии. На рисунке 2 при n = 5, 10, 20, 1000 представлены распределения G(S_n|H₀)  статистики S_K в случае проверки аналогичной, но уже сложной, гипотезы о нормальности, когда по выборке вычисляют оценки максимального правдоподобия (ОМП) параметров нормального закона.

            При малых n наибольшие отклонения от предельных распределений наблюдаются на “хвостах”. И при простых, и при сложных гипотезах с ростом n распределения G(S_n|H₀)  равномерно сходятся к предельному. Но если в случае простых гипотез с ростом n увеличивается вероятность больших значений статистик, то в случае сложных возрастают вероятности и больших, и малых значений статистик. Последнее замечание справедливо для распределений статистик S_K, S_w , S_W.

Рисунок 2 – Зависимость от n распределений G(S_n|H₀)  статистики S_K Колмогорова при сложной гипотезе (H₀ - нормальное распределение, ОМП): n = 5, 10, 20, 1000

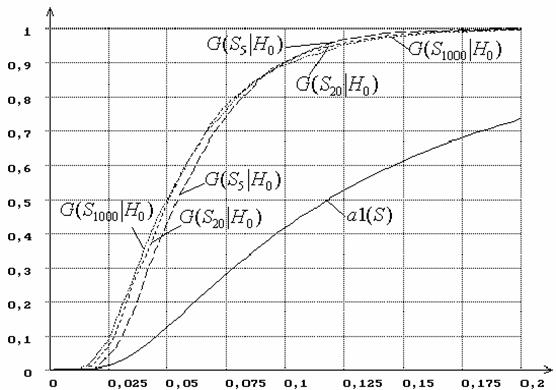
Рисунок 3 иллюстрирует изменения с ростом n распределений G(S_n|H₀)  статистики Крамера-Мизеса-Смирнова S_w при проверке сложной гипотезы о нормальности и использовании при оценивании параметров метода максимального правдоподобия. Чтобы подчеркнуть разницу в распределениях статистик при простых и сложных гипотезах, на указанном рисунке приведены G(S_n|H₀)  для n = 5, 20, 1000 и a1(S) – предельная функция распределения статистики S_w при проверке простой гипотезы.

            Таким образом, распределения G(S_n|H₀)  статистик непараметрических критериев при простых и сложных гипотезах с ростом n очень быстро сходятся к предельным, и уже при n ³15-20 можно, не опасаясь больших ошибок, пользоваться этими предельными законами при анализе данных.

Однако последний вывод не означает, что при малых объемах выборок с помощью этих критериев можно успешно различать близкие гипотезы. Для надежного различения близких законов распределения, в частности с помощью критерия согласия Колмогорова, может потребоваться выборка достаточно большого объема [30].

Рисунок 3 – Зависимость от n распределений G(S_n|H₀)   статистики S_w Крамера-Мизеса-Смирнова при сложной гипотезе (H₀ - нормальное распределение, ОМП): n = 5, 20, 1000

[Предыдущая][Содержание][Следующая]