3.2
Порядок проверки сложной гипотезы о согласии
При проверке согласия опытного распределения с теоретическим распределением случайной величины X действуют следующим образом.
а) Формулируют проверяемую гипотезу, выбирая теоретическое распределение F(x,q) случайной величины, согласие которого с опытным распределением этой величины следует проверить. Перечень теоретических распределений, для которых возможна проверка сложных гипотез с использованием данных рекомендаций, приведен в 3.2.7.
б) Из совокупности отбирают случайную выборку объема n. Полученные результаты наблюдений располагают в порядке их возрастания, так что в распоряжении имеют упорядоченную выборку значений
x1 £ x2 £ … £ xn.
в) По выборке вычисляют оценки параметров распределения F(x,q), выбранного в п.а [оценки максимального правдоподобия на основании формул (21)-(23) или MD-оценки, минимизирующие статистику критерия на основании, соответственно, формул (24), (25) или (26)].
г) В соответствии с выбранным критерием проверки вычисляют значение статистики S* критерия [статистику Колмогорова, Смирнова, w2 Мизеса или W2 Мизеса по формулам (6), (12), (15) или (16)].
е) В соответствии с выбранным критерием проверки, теоретическим распределением F(x,q), оцененным параметром или параметрами, используемым методом оценивания определяют распределение статистики критерия G(S|H0) при справедливости гипотезы H0.
ж) На основании выбранного в п. 5 распределения G(S|H0) вычисляют значение
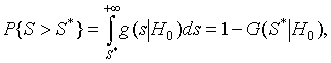
где G(S|H0) – распределение статистики критерия при справедливости гипотезы H0.
a) Если P{S>S*}>a , где a – задаваемый уровень значимости, то нет оснований для отклонения проверяемой гипотезы. В противном случае проверяеjмая гипотеза H0 отвергается. Можно вычисленное значение статистики S* сравнить с критическим значением Sa , определяемым из условия
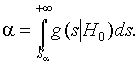
Гипотеза о согласии отвергается, если значение статистики попадает в критическую область, т. е. при S* > Sa .
Если закон распределения, относительно которого проверяют гипотезу о согласии с использованием непараметрического критерия, не входит в перечень приведенный в 3.2.7, то для построения распределения статистики G(S|H0), соответствующего проверяемой гипотезе H0, рекомендуется воспользоваться методикой компьютерного анализа, изложенной в 2.3.2.